Подготовка к ЕГЭ и ОГЭ

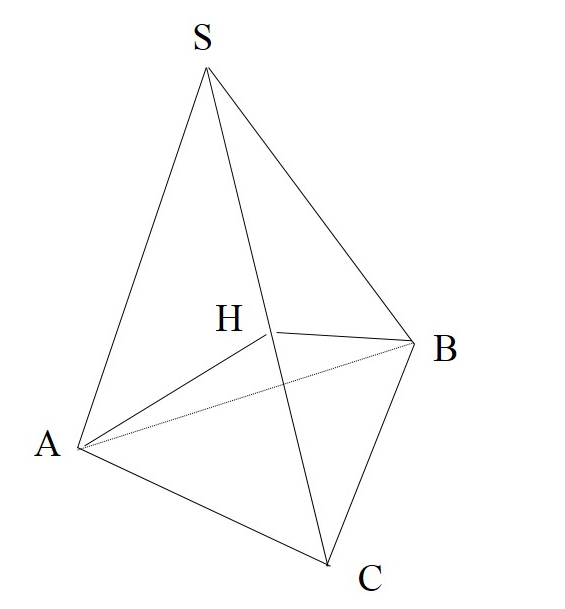
Дано: SABC -пирамида, \( \large \angle ASB=60^\circ, \angle BSC=\angle CSA \: \)\( \large =45^\circ \: \), \( \large r \: \) - радиус вписанной в пирамиду сферы, \( \large SA=SB=2, SC=2\sqrt 2 \: \).

а) Доказать, \( \large (BSC)\bot (ASC) \: \)

б) Найти \( \large r \: \)

а) Т.к. AS=SB, то треугольник \( \large ASB \: \)-равнобедренный. Следовательно, \( \large \angle SAB=\angle SBA=\frac{180^\circ-60^\circ}2=60^\circ \: \). Т.к. все углы треугольника равны 60,то треугольник ASB-равносторонний, т.е. \( \large AC=CB=AB \: \).

\(\bigtriangleup ASC=\bigtriangleup BSC \: \) (по первому признаку равенства треугольников, т.к. AS=CB, \(\angle ASC=\angle CSB \: \), SC-общая). Следовательно, AC=BC.

\(\bigtriangleup SCB: \: \) по теореме косинусов имеем, что

\(BC^2=SC^2+BS^2 \: \) \(-2\cdot SC\cdot BS\cdot cos(\angle CSB) \: \)

\(BC^2=8+4-2\cdot2\sqrt2\cdot 2\cdot\frac{\sqrt2}2\Rightarrow \: \) \(BC^2=4\Rightarrow BC=2 \: \)

т.е. BC=AC=2,SB=AS=2. Следовательно, \( \large \bigtriangleup ASC,\bigtriangleup SCB \: \) - равнобедренные \( \large \Rightarrow\angle SCA=\angle SCB=45^\circ \: \) \( \large \Rightarrow\;\angle SAC=\angle SBC=90^\circ \: \)

Проведем \( \large BH\bot SC \: \), то есть высоту в треугольнике \( \large ASC \: \). Имеем, что AH-высота треугольника BSC. т.е. \( \large BH\bot SC AH\bot SC \: \). Имеем по определению двугранный угол AHB,причем в треугольнике AKB \( \large AH=HB=\sqrt 2 \: \). По теореме косинусов найдем \( \large \angle AHB \: \) и получим,что \( \large \angle AHB=90^\circ \: \). Следовательно, и двугранный угол \( \large \angle AHB=90^\circ \: \), т.е. искомые плоскости перпендикулярны, что и требовалось доказать.

б) Чтобы найти радиус вписанной сферы, воспользуемся следующей формулой: \( \large r=\frac{V_{пир}}{S_{полн}} \: \)

Найдем объем пирамиды:

\(V_{пир}=\frac13S_{SBC}\times AH= \: \) \(\frac13\cdot (\frac12\cdot2\cdot 2) \: \) \(\times\sqrt2=\frac{2\sqrt2}3 \: \)

Найдем площадь всей поверхности пирамиды:

\(S_{полн}=2\times S_{ASB}+2\times S_{ASC}= \: \) \(2\cdot\frac{4\sqrt3}4+2\cdot\frac12\cdot2\cdot2 \: \) \(=2\sqrt3+4 \: \)

\(r=\frac{3\cdot2\sqrt2}{3\cdot(2\sqrt3+4)}=\frac{\sqrt2(\sqrt3-2)}{3-4}= \: \) \(\sqrt8-\sqrt6 \: \)

Ответ: \( \large \sqrt8-\sqrt6 \: \)

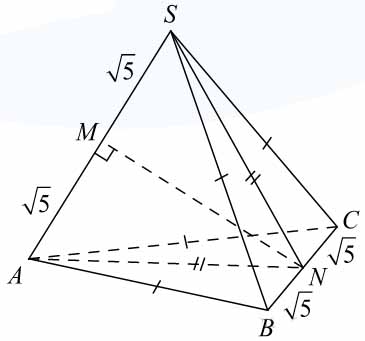
а) Заметим, что треугольники \( \large SBC \: \) и \( \large АВС \: \) равны по трем сторонам. Они являются равнобедренными и имеют общее основание. Проведем медианы \( \large SN \: \) и \( \large AN \: \) к этому основанию. Они попадут в одну точку точку \( \large N \: \), которая является серединой \( \large ВС \: \) и будут являться высотами данных треугольников. Тем самым, прямая \( \large BC \: \) перпендикулярна двум пересекающимся прямым плоскости \( \large ASN \: \), а значит, и всей этой плоскости. Но тогда прямая \( \large ВС \: \) перпендикулярна любой прямой плоскости \( \large ASN \: \). В частности, перпендикулярна прямой \( \large SA \: \).

б)

Построим высоту \( \large NМ \: \) треугольника \( \large ASN \: \). Заметим, что \( \large NМ \: \) является общим перпендикуляром прямых \( \large AS \: \) (по построению) и \( \large ВС \: \), поскольку \( \large NМ \: \) лежит в плоскости \( \large ASN \: \). Тогда длина \( \large NМ \: \) и есть искомое расстояние между скрещивающимися прямыми \( \large AS \: \) и \( \large ВС \: \).

Заметим, что \( \large SN = AN = \sqrt{17-5}=\sqrt{12} \: \). Тогда треугольник \( \large SNA \: \) равнобедренный, его высота \( \large NМ \: \) является также медианой, а тогда из прямоугольного треугольника \( \large АМN \: \) находим: \( \large NM=\sqrt{AN^2-AM^2} = \sqrt{12-5} \: \) \( \large = \sqrt7 \: \).

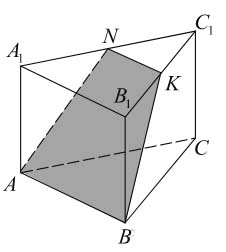
а) Проведём через точку \( \large N \: \) прямую, параллельную прямой \( \large AB \: \), до пересечения с прямой \( \large B_1C_1 \: \) в точке \( \large K \: \). Трапеция \( \large ABKN \: \) — искомое сечение.

б) Имеем \( \large A_1N= 3 \: \), так как точка \( \large N \: \) — середина ребра \( \large A_1C_1 \: \). Значит, \( \large AN =\sqrt{16+9} = 5 \: \). Аналогично \( \large BK = 5 \: \).

Далее \( \large NK = 3 \: \), как средняя линия треугольника \( \large A_1B_1C_1 \: \). Следовательно, искомый периметр сечения равен \( \large 6 + 5 + 5 + 3 = 19 \: \).

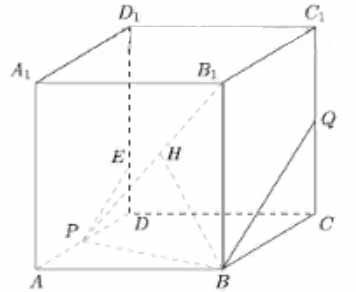
а) Пусть ребро куба равно \( \large 4a \: \). Отметим на ребре \( \large DD_1 \: \) такую точку \( \large E \: \), что \( \large DE = a \: \). Прямая \( \large PE \: \) параллельна прямой \( \large BQ \: \), следовательно необходимо проверить, что \( \large \angle EPB_1 =90^0 \: \).

По теореме Пифагора вычислим длину стороны треугольника \( \large EPB_1 \: \):

\(PE^2 = PD^2+DE^2=5a^2. \: \)

\(B_1E^2 =B_1D_1^2+D_1E^2=32a^2+9a^2=41a^2 \: \)

\(B_1P=D_1B^2+BA^2+AP^2=16a^2+16a^2+4a^2=36a^2 \: \),

\(B_1P=6a \: \).

а) Поскольку \( \large 5a^2+36a^2=41a^2=B_1E^2=PE^2+B_1P^2 \: \), по теореме, обратной теореме Пифагора, получаем, что \( \large EPB_1=90^0 \: \), т.е. прямая \( \large BQ \: \) перпендикулярна прямой \( \large B_1P \: \).

б) Поскольку прямая \( \large BQ \: \) перпендикулярна прямой \( \large B_1P \: \), проекции точек \( \large B \: \) и \( \large Q \: \) на прямую \( \large B_1P \: \) совпадают. В прямоугольном треугольнике \( \large BB_1P \: \) имеем:

\(cos \angle HB_1B=\frac{HB_1}{B_1B}=\frac{B_1B}{PB_1} \: \), откуда \(HB_1=\frac{B_1B^2}{PB_1}=\frac{576}{36} =16 \: \).

Другое решение:

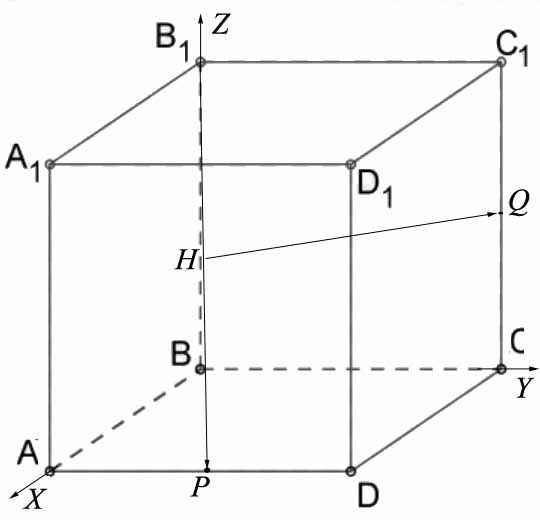
Введем систему координат с центром в точке \( \large B \: \). Оси \( \large X \: \), \( \large Y \: \), \( \large Z \: \) направим соответственно вдоль ребер куба \( \large BA \: \), \( \large BC \: \),\( \large BB_1 \: \). Пусть длина ребра куба равна \( \large a \: \). Тогда координаты точек \( \large B_1(0,0,a) \: \), \( \large P(0,\frac{a}{2}, 0) \: \), \( \large Q(0,a,\frac{a}{2}) \: \). Следовательно, \( \large \overrightarrow{B_1P}(a,\frac{a}{2},-a) \: \), \( \large \overrightarrow{BQ}(0,a,\frac{a}{2}) \: \). Их скалярное произведение:

\(\overrightarrow{BQ}(0,a,\frac{a}{2}) \cdot \overrightarrow{BQ}(0,a,\frac{a}{2}) = a\cdot 0+ \frac{a}{2}\cdot a+ (-a)\cdot \frac{a}{2} = 0 \: \). Следовательно, они перпендикулярны.

б) Уравнение прямой \( \large B_1P \: \), проходящей через две точки, имеет вид:

$$\frac{x}{a} = \frac{y}{\frac{a}{2}} = \frac{z-a}{-a}$$

Откуда

$$\begin{cases}z=-x+a \\y=\frac{1}{2}\cdot x\end{cases}\;(1)$$

Путь точка \( \large H \: \) - проекция точки \( \large Q \: \) на эту прямую, т.е. точка \( \large H \: \) лежит на прямой, а значит, ее координаты удовлетворяют уравнению прямой \( \large B_1P \: \), с одной стороны, а с другой, вектор \( \large \overrightarrow{B_1P} \perp \overrightarrow{QH}(x_h,y_h-a,z_h-\frac{a}{2}) \: \), т.е. их скаляное произведение равно нулю:

$$ a\cdot x_h+\frac{a}{2}\cdot (y_h-a)+(-a)\cdot (z_h-\frac{a}{2}) =0 $$Подставляем в это уравнение координаты точки \( \large H \: \), выраженные (1):$$ a\cdot x_h+\frac{a}{2}\cdot \left( \frac{1}{2}\cdot x_h-a \right)+(-a)\cdot \left(-x_h+a -\frac{a}{2}\right) =0 $$

Найдем:

\(x_h=\frac{4a}{9} \Rightarrow y_h=\frac{2a}{9}, z_h=\frac{5a}{9} \: \)

Тогда расстояние \( \large HB_1 =\sqrt{\left(0 - \frac{4a}{9}\right)^2+\left(0 - \frac{2a}{9}\right)^2+\left(a - \frac{5a}{9}\right)^2} = \: \) \( \large \sqrt{\left( \frac{16a^2}{81}\right)+\left( \frac{4a^2}{81}\right)+\left( \frac{16a^2}{81}\right)} = \: \)

\(\sqrt{\frac{36a^2}{81}} =\frac{6a}{9} =\frac{6\cdot 24}{9} =16 \: \)

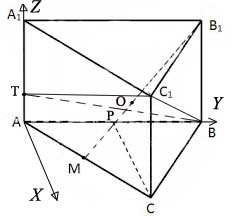
Введм декартовую систему координат с центром в точка \( \large A \: \), а оси направим так, чтобы ось \( \large Y \: \) была в направлении полупрямой \( \large [AB) \: \), ось \( \large Z \: \) вдоль ребра \( \large [AA_1) \: \), а ось \( \large X \: \) в полуплоскость относительно прямой \( \large AB \: \), содержащей току \( \large C \: \).

1) Напишем уравнение плоскости \( \large ВТС_1 \: \) в данной системе координат.

Так как треугольник \( \large ABC \: \) по условию правильный, то координата \( \large x_с \: \) точки \( \large C \: \) будет равна медиане \( \large PC \: \) треугольника \( \large ABC \: \), т.е. \( \large 4\cdot \frac{\sqrt3}{2} \: \) \( \large =2\sqrt3 \: \). Таким образом, \( \large C(2\sqrt3, 2, 0) \: \), \( \large T(0,0,3) \: \), \( \large B(0,4,0) \: \), \( \large C_1(2\sqrt3, 2, 9) \: \).

Так как уравнение плоскости \( \large \Large \alpha \cdot x+\beta\cdot y +\gamma\cdot z +\delta =0 \: \), то подставляя в это уравнение координаты найденных точек найдем уравнение плоскости:

$$ \displaystyle\begin{cases}C: 2\sqrt3\cdot \alpha+2\beta+9\gamma+\delta = 0\\T: 3\cdot \gamma+\delta = 0\\B: 4\cdot \beta+\delta = 0\end{cases}\Leftrightarrow\:\begin{cases}\gamma = \frac{4}{3}\beta\\\delta = - 4\beta\\\alpha = -\frac{10}{2\sqrt3}\beta\end{cases}$$

Откуда получаем после сокращение на \( \large \beta \neq 0 \: \):

\( \displaystyle -\frac{5}{\sqrt3}x+y+\frac{4}{3}z-4 = 0 \: \).

2) Напишем уравнение прямой \( \large MB_1 \: \). Координаты точки \( \large M \: \) - среднее арифметическое координат точек \( \large C \: \) и \( \large A \: \): \( \large M(\sqrt3;1;0) \: \), коодинаты \( \large B_1(0;4;9) \: \). Пусть точка \( \large O(x_o,y_o,x_o) \: \) - точка пересечения прямой \( \large MB_1 \: \) и плоскости \( \large ВТС_1 \: \). Тогда из уравнения прямой, проходящей через две точки:

\(\displaystyle \frac{x_o - x_M}{x_B - x_M} = \frac{y_o - y_M}{y_B - y_M} =\frac{z_o - z_M}{z_B - z_M} =k \: \) получим:

$$\begin{cases}x_o -x_M = k\cdot (x_B-x_M)\\y_o -y_M = k\cdot (y_B-y_M)\\z_o -z_M = k\cdot (z_B-z_M)\end{cases}$$

С другой стороны, точка \( \large O \: \) лежит на плоскости:

\(\alpha x_0+\beta y_0+\gamma z_0+\delta = 0 \: \), т.е. выражая \(x_o,y_o,z_o \: \) из системы и подставляя их в уравнение плоскости, получим уравнение относительно \(k \: \):

\(\alpha \cdot(k\cdot (x_B-x_M)+x_M) + \beta \cdot(k\cdot (y_B-y_M)+y_M) + \gamma \cdot(k\cdot (z_B-z_M)+z_M)= 0 \: \), откуда:

\(\displaystyle k = \frac{-\delta - \alpha\cdot x_M -\beta\cdot y_M -\gamma\cdot z_M}{\alpha \cdot (x_B-x_M)+\beta \cdot (y_B-y_M)+\gamma \cdot (z_B-z_M)} \: \).

Тогда \( \large OM = |k|\sqrt{(x_B-x_M)^2+(y_B-y_M)^2+(z_B-z_M)^2} \: \).

В нашем случае, \( \large \displaystyle k=\frac{-(-4)-(-\frac{5}{\sqrt3})\cdot \sqrt3-1\cdot 1-\frac{4}{3}\cdot 0}{-\frac{5}{\sqrt3}\cdot(-\sqrt3)+1\cdot3+\frac{4}{3}\cdot 9}=\frac{8}{20} = \frac{2}{5} \: \)

\(OM = \frac{2}{5}\sqrt{3+9+81} = \frac{2}{5}\sqrt{93} \: \).

Тогда большее расстояние \( \large OB_1 = \frac{3}{5}\sqrt{93} \: \)

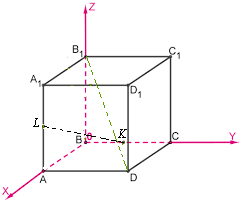
а) Введем систему координат с центром в точке \( \large B \: \). Ось \( \large X \: \) направим вдоль ребра \( \large BA \: \), ось \( \large Y \: \) вдоль ребра \( \large BC \: \), а ось \( \large Z \: \) вдоль ребра \( \large BB_1 \: \).

В этой ситеме координат определим координаты векторов \( \large \overrightarrow{B_1D} \: \) и \( \large \overrightarrow{LK} \: \) и покажем, что их скалярное произведение равно нулю.

Для определения координат векторов \( \large \overrightarrow{B_1D} \: \) и \( \large \overrightarrow{LK} \: \) найдем координаты точек \( \large B_1 \: \), \( \large D \: \), \( \large L \: \) и \( \large K \: \).

Пусть длина ребра куба равна некоторому \( \large a \: \). Тогда координаты \( \large B_1(0,0,a) \: \), \( \large D(a,a,0) \: \), \( \large L(a,0,\frac{a}{2} \: \), \( \large K(0,\frac{a}{2},0) \: \).

Тогда \( \large \overrightarrow{B_1D}(a-0,a-0,0-a) = \: \) \( \large \overrightarrow{B_1D}(a,a,-a) \: \), \( \large \overrightarrow{LK}(0-a,\frac{a}{2}-0,0-\frac{a}{2}) = \: \) \( \large \overrightarrow{LK}(-a,\frac{a}{2},-\frac{a}{2}) \: \).

Тогда скалярное произведение векторов: \( \large \overrightarrow{B_1D}(a,a,-a)\cdot \overrightarrow{LK}(-a,\frac{a}{2},-\frac{a}{2}) = -a^2+\frac{a^2}{2}+\frac{a^2}{2} =0 \: \). Таким образом, вектора перпендикулярны, а, значит, и прямые на которых они лежат.

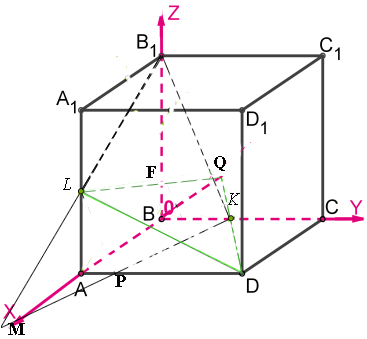
б) Для решения б) напишем уравнение влоскостей \( \large B_1LK \: \) и \( \large DLK \: \). Так как уравнение плоскости в общем виде имеет вид: \( \large \alpha \cdot x + \beta \cdot y + \gamma \cdot z + \delta = 0 \: \), то для определения уравнения плоскости воспользуемся условием, что плоскость \( \large B_1LK \: \) проходит через точки \( \large B_1 \: \), \( \large L \: \) и \( \large K \: \). Т.е , если мы подставим координаты этих точек в уравнение плоскости должно получиться тождество. Тогда:

$$\begin{cases}K: \alpha \cdot 0 + \beta \cdot \frac{a}{2} + \gamma \cdot 0 + \delta = 0, \\L: \alpha \cdot a + \beta \cdot 0 + \gamma \cdot \frac{a}{2} + \delta = 0, \\B_1: \alpha \cdot 0 + \beta \cdot 0 + \gamma \cdot 0 + \delta = 0,\end{cases}\quad\Rightarrow\quad\begin{cases}\alpha = \frac{1}{2}\cdot \gamma \\\beta = 2 \cdot\gamma,\\\delta = -a\cdot \gamma,\end{cases}$$

Подставляем эти значения в общий вид уравнения плоскости, получим, уравнение плоскости \( \large B_1LK \: \):

$$ \frac{1}{2}\cdot \gamma\cdot x + 2 \cdot\gamma \cdot y + \gamma \cdot z - a\cdot \gamma = 0 $$И после сокращение на \( \large \gamma (\gamma\neq 0) \: \), окончательно получаем:$$ \frac{1}{2}\cdot x + 2 \cdot y + z - a = 0 $$

Аналогично,

$$\begin{cases}K: \alpha \cdot 0 + \beta \cdot \frac{a}{2} + \gamma \cdot 0 + \delta = 0, \\L: \alpha \cdot a + \beta \cdot 0 + \gamma \cdot \frac{a}{2} + \delta = 0, \\D: \alpha \cdot a + \beta \cdot a + \gamma \cdot 0 + \delta = 0,\end{cases}\quad\Rightarrow\quad\begin{cases}\gamma = 2 \cdot\ \beta \\\alpha = - \frac{\beta}{2},\\\delta = - \frac{\beta}{2},\end{cases}$$

Подставляем эти значения в общий вид уравнения плоскости, получим, уравнение плоскости \( \large DLK \: \):

$$ -\frac{\beta}{2} \cdot x + \beta \cdot y + 2\beta \cdot z - \frac{\beta}{2} = 0 $$И после сокращение на \( \large \beta (\beta\neq 0) \: \), окончательно получаем:$$ -\frac{1}{2} \cdot x + y + 2\cdot z - \frac{1}{2} = 0 $$

Как известно, угол между плоскостями - это угол между их нормальными векторами. Так как нормальный вектор плоскости \( \large B_1LK \: \), как следует из ее уравнения: \( \large \vec n (\frac{1}{2}, 2,1) \: \), а нормальный вектор \( \large DLK \: \): \( \large \vec m (-\frac{1}{2}, 1,2) \: \), то угол между векторами:

$$ cos \angle (\vec n,\vec m = \frac{-\frac{1}{2}\cdot \frac{1}{2} + 1\cdot 2 + 2\cdot 1 }{\sqrt {\left(\frac{1}{2}\right)^2+2^2+1^2} \cdot \sqrt {\left(-\frac{1}{2}\right)^2+1^2+2^2} } =$$$$ = \frac{\frac{15}{4}}{\frac{21}{4}} = \frac{15}{21} = \frac{5}{7}$$