Подготовка к ЕГЭ и ОГЭ

\(4^x+\frac{16}{x^2}\geq5\times\frac{2^{x+1}}x \: \)

\(2^{2x}+\frac{16}{x^2}\geq10\times\frac{2^x}x \: \)

Домножим обе части на \( \large \frac x{2^x} \: \). Получим 2 случая:

1) \( \large 2^x\times x+\frac{16}{2^x\times x}\geq10 \: \)

Пусть \( \large y=2^x\times x \: \). Тогда \( \large y+\frac{16}y\geq10 \: \)

\(\frac{y^2+16-10y}y\geq0 \: \)

Нули числителя: \( \large y^2+16-10y=0 \: \)

\(D=100-16\cdot4=100-64=36 \: \). Откуда \(y_1=8, y_2=2 \: \).

Получаем тогда:

\(\frac{(y-8)(y-2)}y\geq0 \: \)

Решая методом интервалов, получим: \( \large (0;1]\bigcup[2;+\infty) \: \)

2) \( \large x<0 \: \) \( \large \frac{y^2+16-10y}y\leq0 \: \) или \( \large \frac{(y-8)(y-2)y}y\leq0 \: \).

Решая методом интервала с учетом: \( \large x<0 \: \) получим, \( \large (-\infty;0) \: \).

Окончательный ответ: \( \large (0;1]\bigcup[2;+\infty)\bigcup (-\infty;0) \: \)

Сделав замену \( \large t=\frac{5x-21}{10} \: \), получаем:

\(\left(\frac1t+t\right)^2\le \frac{25}{4} \: \) \(\Rightarrow \: \) \(-\frac{5}{2} \le \frac{1}{t}+ t \le \frac{5}{2} \: \) \(\Rightarrow \: \) \(-5\le \frac{2t^2+2}{t}\le 5 \: \) \(\Rightarrow \: \) \(\begin{cases} \frac{2t^2-5t+2}{t} \le 0, \\ \frac{2t^2 + 5t+2}{t} \ge 0 \end{cases} \: \) \(\Rightarrow \: \) \(\begin{cases} \frac{2(t-2)(t-\frac12)}{t} \le 0, \\ \frac{2(t +2)(t + \frac12)}{t} \ge 0 \end{cases} \: \) \(\Rightarrow \: \) \(\left[\begin{array}{l}-2 \le t \le -\frac12\\\frac12 \le t \le 2\end{array}\right. \: \)/

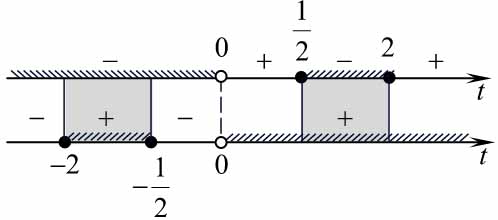
Возвращаясь к исходной переменной, получаем:

\(\left[\begin{array}{l}5\le5x-21\le20\\-20\le 5x-21\le -5 \end{array}\right. \: \) \(\Rightarrow \: \) \(\left[\begin{array}{l}\frac{26}{5}\le x \le \frac{41}{5},\\ \frac15 \le x \le \frac{16}{5} \end{array}\right. \: \)

Воспользуемся тем, что для суммы \( \large |a|+|b| \: \) возможны четыре случая раскрытия модулей, откуда заключаем:

\(|a|+|b| \le c \Leftrightarrow \begin{cases} -c\le a+b\le c\\ -c\le a- b\le c \end{cases} \: \).

Тогда имеем:

\(3|x+3|+|2-x|\le 3x+14 \Leftrightarrow \: \) \( \begin{cases} -3x-14\le 3(x+3) + (2-x)\le 3x+14\\ -3x-14\le 3(x+3) - (2-x)\le 3x+14\end{cases} \: \) \(\Leftrightarrow \: \) \( \begin{cases} -3x-14\le 2x+11\le 3x+14\\ -3x-14\le 4x+7\le 3x+14\end{cases} \: \) \(\Leftrightarrow \: \) \( \begin{cases} x\ge -5\\ x\ge -3 \Leftrightarrow -3 \le x \le 7\\ x\le 7\end{cases} \: \)