Подготовка к ЕГЭ и ОГЭ

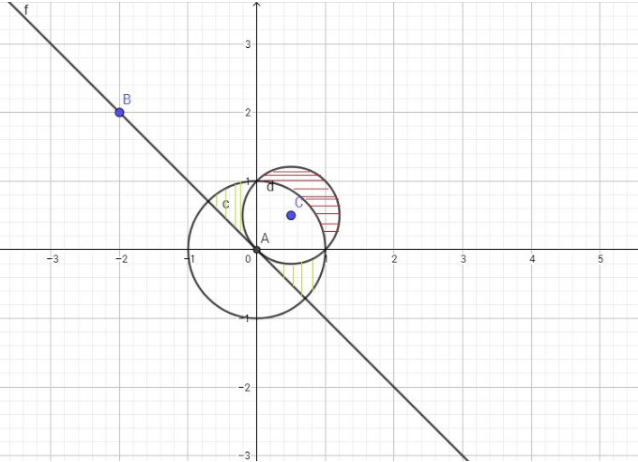
ОДЗ:

\(x+y>0 \: \), \(y>-x \: \)

\(x^2+y^2>0 \: \) всегда, кроме x=0; y=0

\(x^2+y^2\neq1 \: \). Окружность с центром \(О_1(0;0) \: \) и радиусом \(R=1 \: \). Изображаем пунктиром.

Преобразуем правую часть уравнения: \( \large 1=log_{x^2+y^2}(x^2+y^2) \: \)

Тогда получим:

\(log_{x^2+y^2}(x+y)> \: \)\(log_{x^2+y^2}(x^2+y^2) \: \)

1 сл: \( \large x^2+y^2>1 \: \)

\(\frac{x+y}{x^2+y^2}>1 \: \)

\(\frac{x+y-x^2-y^2}{x^2+y^2}>0 \: \)

\(\frac{-x-y+x^2+y^2}{x^2+y^2}<0 \: \)

\(-x-y+x^2+y^2<0 \: \)

\(\left(x-\frac12\right)^2+\left(y-\frac12\right)^2>\frac12 \: \)

Окружность с центром в точке (1/2;1/2) и радиусом \( \large R=\frac1{\sqrt2} \: \) при \( \large x^2+y^2>1 \: \)

2 сл. \( \large 0 < x^2+y^2 < 1 \: \)

\(\frac{x+y}{x^2+y^2}<1 \: \)

\(\frac{x+y-x^2-y^2}{x^2+y^2}<0 \: \)

\(\frac{-x-y+x^2+y^2}{x^2+y^2}>0 \: \)

\(-x-y+x^2+y^2>0 \: \)

\(\left(x-\frac12\right)^2+\left(y-\frac12\right)^2>\frac12 \: \)

Окружность с центром в точке (1/2;1/2) и радиусом \( \large R=\frac1{\sqrt2} \: \) при \( \large 0 < x^2+y^2 < 1 \: \) (см. рисунок)

Найдем площадь полученной фигуры:

\(S_{green}=\frac12S_{бол\;окр}-(\frac12S_{мал\;окр}+ \: \)

\((\frac14S_{бол}-S_{прям\;треуг}) \: \) \(=\frac\pi2-(\frac\pi4+(\frac\pi4-\frac12)=\frac12 \: \)

\(S_{red}=\frac12S_{мал\;окр}- \: \) \((\frac14S_{бол}- \: \) \(S_{прям\;треуг})=\frac\pi4- \: \) \((\frac\pi4-\frac12)= \: \) \(\frac12 \: \)

\(S_{полн}=S_{green}+S_{red}=\frac12+\frac12 \: \) \(=1 \: \)

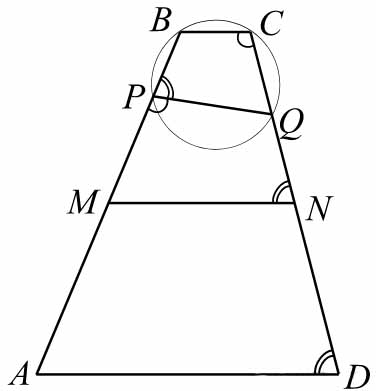
a) По условию, четырёхугольник \( \large PBCQ \: \) вписанный. Значит \( \large \angle BCQ +\angle BPQ = 180^0 \: \), Отрезок \( \large MN \: \) — средняя линия трапеции \( \large ABCD \: \), она параллельна основанию \( \large BC \: \), а тогда \( \large \angle BCQ +\angle QNP = 180^0 \: \) как односторонние углы при параллельных прямых. Следовательно,\( \large \angle BPQ = \angle QNM \: \) Для смежных углов справедливо равенство \( \large \angle BPQ +\angle MPQ = 180^0 \: \) а значит, \( \large \angle QNM +\angle MPQ = 180^0 \: \) В четырёхугольнике \( \large MPQN \: \) сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Тем самым, точки \( \large M \: \), \( \large N \: \), \( \large P \: \) и \( \large Q \: \) лежат на одной окружности, что и требовалось доказать.

б)

Пусть \( \large \angle QNM = \angle QDA =\alpha \: \) (эти углы равны как соответственные углы при параллельных прямых).

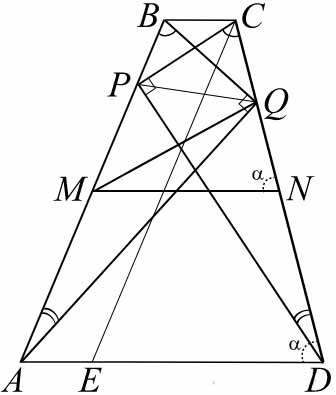
В пункте а) было показано, что \( \large \angle QNM +\angle MPQ = 180^0 \: \), это означает, что \( \large \angle QDA +\angle MPQ = 180^0 \: \) , и, следовательно, точки \( \large A \: \), \( \large D \: \), \( \large P \: \) и \( \large Q \: \) тоже лежат на одной окружности.

Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны. Следовательно, \( \large \angle BPQ =\angle PCQ \: \) и \( \large \angle PAQ =\angle PDQ \: \) . Значит, треугольники \( \large DPC \: \) и \( \large AQB \: \) подобны по двум углам. Следовательно, \( \large \angle AQB =\angle DPC =90^0 \: \), так как по условию \( \large DP \: \) и \( \large PC \: \) перпендикулярны.

В прямоугольном треугольнике \( \large AQB \: \) точка \( \large M \: \) − середина гипотенузы. Следовательно, \( \large MQ =AM =MB = \: \) \( \large \frac{AB}{2} = \frac{21}{2} =10,5 \: \). С другой стороны, средняя линия трапеции \( \large MN = \frac{AD+BC}{2} = \frac{4+17}{2} =10,5 \: \). Значит, треугольник \( \large NMQ \: \) равнобедренный и в нём \( \large QN=2\cdot MN\cdot cos\alpha = 21\cdot cos\alpha \: \). Осталось найти косинус угла \( \large CDA \: \).

Для этого на отрезке \( \large AD \: \) отметим точку \( \large E \: \), так что \( \large AE=BC=4 \: \), тогда \( \large DE=13 \: \), \( \large CE=21 \: \). Для треугольника \( \large CDE \: \) запишем теорему косинусов: \( \large CE^2 =DE^2 +CD^2- \: \) \( \large 2DE\cdot CD\cdot cos\alpha \: \), откуда выразим косинус угла \( \large CDE \: \):

\(cos\alpha = \frac{DE^2+CD^2-CE^2}{2DE\cdot CD}= \: \) \(\frac{13^2+20^2-21^2}{2\cdot 13\cdot20}=\frac{16}{65} \: \).

Итак, \( \large QN = 21cos\alpha=21\cdot \frac{16}{65} = \frac{336}{65} \: \).

Приведем другое решение пункта б):

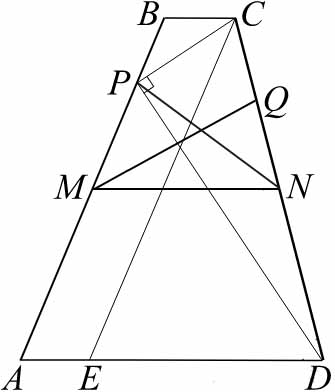
Заметим, что раз треугольник \( \large PDC \: \) — прямоугольный, то \( \large PN=CN=ND=10 \: \), \( \large MN=\frac{17+4}{2}=10,5 \: \) - средняя линия трапеции \( \large ABCD \: \). Зная боковые стороны и основания трапеции, нетрудно найти ее высоту из треугольника \( \large CED \: \) со сторонами 21, 20 и 13:

\(h=\frac{252}{13} \: \). Отсюда найдем \(sin\angle BAD = \frac{\frac{252}{13}}{21}=\frac{12}{13} \: \), \(sin\angle CDA=\frac{\frac{252}{13}}{20}=\frac{63}{65} \: \). Теперь, так как \(\angle PNM = \angle BAD \: \), по теореме синусов для треугольника \(MPN \: \), можем найти радиус окружности, описанной около \(MPQN \: \):

\(R=\frac{PN}{2sin\angle PMN}=\frac{10}{2\cdot \frac{12}{13}} = \frac{65}{12} \: \).

Так как найдем \( \large \angle QNM = \angle CDA \: \), найдем \( \large MQ \: \) по теореме синусов для треугольника \( \large MQN \: \):

\(MQ=2Rsin\angle QNM= \: \) \(2\cdot\frac{65}{12}\cdot \frac{63}{65} \: \) \( = \frac{21}{2} \: \);

Таким образом, треугольник \( \large MQN \: \) — равнобедренный:

\(QN=2\cdot MN\cdot cos\angle MNQ = \: \) \( 2\cdot \frac{21}{2}\cdot \sqrt{1-\left( \frac{63}{65}\right)^2} = \: \)

\(21\cdot \frac{\sqrt{65^2-63^2}}{65} = \frac{21}{65}\sqrt{2\cdot 128} = \: \) \(\frac{21\cdot 16}{65} =\frac{336}{65} \: \).

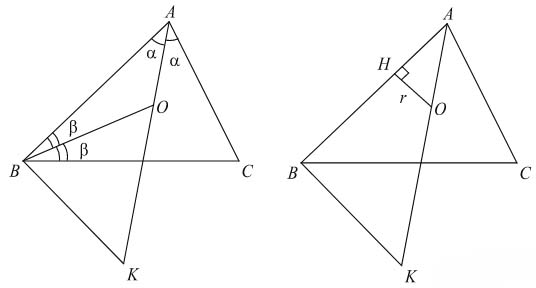
а) Пусть \( \large \angle A=2\alpha \: \), \( \large \angle B=2\beta \: \) Так как \( \large O \: \) — центр вписанной окружности треугольника \( \large ABC \: \) то \( \large AO \: \), \( \large BO \: \) — биссектрисы углов \( \large A \: \) и \( \large B \: \), значит, \( \large \angle BAO =\alpha \: \), \( \large \angle ABO =\beta \: \). Угол \( \large BOK \: \) внешний для треугольника \( \large AOB \: \) поэтому \( \large \angle BOK =\alpha + \beta \: \) (см. рисунок слева).

Так как \( \large BK = OK \: \) (по построению), то \( \large \angle OBK =\angle BOK =\alpha + \beta \: \), тогда \( \large \angle CBK = \angle OBK - \angle CBO = \alpha + \beta - \beta = \alpha \: \). Углы \( \large CBK \: \) и \( \large KAC \: \) опираются на один и тот же отрезок \( \large CK \: \) и равны друг другу: \( \large \angle CBK = \angle KAC = \alpha \: \). Тогда по признаку, связанному со свойством вписанных углов, точки\( \large A \: \), \( \large B \: \),\( \large K \: \),\( \large C \: \), лежат на одной окружности.

б) Обозначим через \( \large r \: \), \( \large R \: \) радиусы вписанной и описанной окружностей треугольника \( \large ABC \: \). Пусть \( \large H \: \) — проекция точки \( \large O \: \) на сторону \( \large AB \: \) (см. рис.), тогда \( \large OH = r \: \), \( \large AO = \frac{r}{sin \alpha} \: \). Так как точки \( \large A \: \), \( \large B \: \),\( \large K \: \),\( \large C \: \) лежат на одной окружности, то радиус описанной окружности треугольника \( \large ABK \: \) совпадает с радиусом описанной окружности треугольника \( \large ABC \: \) и равен \( \large R \: \).

Из треугольника \( \large ABK \: \) по теореме синусов \( \large \frac{BK}{sin \alpha}=2R \: \), \( \large sin \alpha = \frac{BK}{2R} \: \). Тогда \( \large AO = \frac{r}{sin \alpha} = \frac{r}{\frac{BK}{2R}} = \frac{r\cdot 2R}{BK} \: \).

Так как \( \large r=3 \: \), \( \large R=12 \: \), \( \large BK = OK =5 \: \), то \( \large AO = \frac{3\cdot 24}{5} = 14,4 \: \).