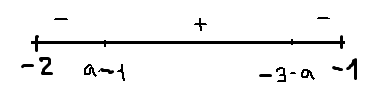
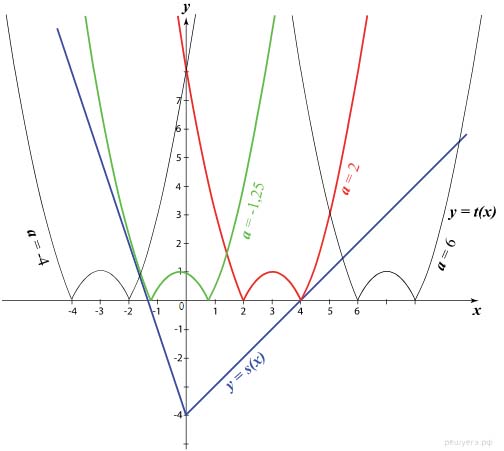
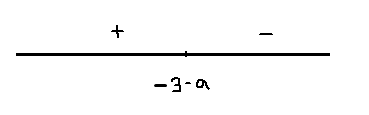Для каждого значения параметра \( \large a \: \) найдите наибольшее значение функции \( \large f\left(x\right)=\left(\left|x\right|-6\right)\cdot x^2+ \: \) \( \large 3\left|x\right|\cdot\left(3-a^2\right)+ \: \) \( \large 6ax \: \) на отрезке \( \large [-3; 3] \: \)
Имеем два случая: 1) \( \large x\geq0 \: \) 2) \( \large x<0 \: \),
1 случай: \( \large x\geq0 \: \). Преобразуем функцию:
\(f(x)=x^3-6x^2+ \: \) \((9+6a-3a^2)x \: \)
Найдем производную функции:
\(f'(x)=3x^2-12x+ \: \) \((9+6a-3a^2) \: \)
\(f'(x)=0 \: \)
\(x^2-4x+3+2a-a^2=0 \: \)
\(D=16-4(3+2a-a^2)= \: \) \(4(a-1)^2 \: \)
\( x_1=3-a \: \), \(x_2=1+a \: \)
Определим знак производной:
1) \( \large 0\lt a\lt 1 \: \); \( \large 1\lt a+1\lt 2 \: \); \( \large 2\lt 3-a \lt 3 \: \)
\(x=a+1 \: \) - точка максимума;
\(fmax=f(a+1)= \: \) \(-2(a+1)(a^2-a-2) \: \)
2) \( \large 1\lt a \lt 2 \: \); \( \large 2 \lt a+1 \lt 3 \: \);\( \large 1\lt3-a\lt2 \: \)
\(x=3-a \: \) - точка максимума
\(fmax=f(3-a)= \: \) \(2(3-a)(6-a) \: \)
3) \( \large 2 \lt a \lt 3 \: \); \( \large 3\lt a+1\lt 4 \: \); \( \large 0 \lt 3-a\lt 1 \: \)
\(x=a+1 \: \) не принадлежит отрезку \(x=3-a \: \)- точка максимума
4) \( \large a>3 \: \)
\(x=a+1, x=3-a \: \), не принадлежат отрезку значений \(x \: \), т.к. т.к. функция убывает, то \(fmax=f(0) \: \)
2 случай: \( \large x\lt 0 \: \). Преобразуем функцию:
\(f(x)=-x^3-6x^2+ \: \) \((-9+6a+3a^2)x \: \)
Найдем производную функции:
\(f'(x)=-3x^2-12x+ \: \) \((-9+6a+3a^2) \: \)
\(f'(x)=0 \: \)
\(x^2+4x+3-2a-a^2=0 \: \)
\(D=16-4(3-2a-a^2)= \: \) \(4(a+1)^2 \: \)
\(x_1=-3-a \: \), \(x_2=-1+a \: \)
Определим знак производной:
1) \( \large -1\lt a\lt 0 \: \);\( \large -3\lt -3-a\lt -2 \: \); \( \large -2\lt a-1\lt -1 \: \)
\(x=a-1 \: \) - точка максимума;
\(fmax=f(a-1)= \: \) \(-2(a-1)(a^2+2a+2) \: \)
2) \( \large -2\lt a\lt -1 \: \); \( \large -3\lt a-1\lt -2 \: \);\( \large -2\lt -3-a\lt -1 \: \)
\(x=-3-a \: \) - точка максимума
\(fmax=f(-3-a)= \: \) \(2a(-3-a)(a+3) \: \)
3) \( \large -3 \lt a\lt -2 \: \); \( \large -4\lt a1\lt -3 \: \);
\(x=-3-a \: \) точка максимума
\(fmax=f(-3-a)= \: \) \(2a(-3-a)(a+3) \: \)
4) \( \large a\lt -3 \: \); \( \large a-10 \: \)
т.к. функция убывает, то \( \large fmax=f(-3)=-9a^2-18a \: \)
Ответ:
при \( \large a\le -3 \: \), \( \large f_{max}=–9a^2–18a \: \);
при \( \large -3\lt a\le-1 \: \), \( \large f_{max}=-2a(a+3)^2 \: \);
при \( \large -1\lt a\le 0, \: \) \( \large f_{max}=2\cdot (a–1) \cdot (a^2+2a+2) \: \);
при \( \large 0\lt a\le1 \: \), \( \large f_{max}=(a+1) \cdot (–2a^2+2a+4)) \: \);
при \( \large 1\lt a\le 3 \: \), \( \large f_{max}=2\cdot (3–a) \cdot (6–a) \: \);
при \( \large a\gt 3 \: \), \( \large f_{max}=0 \: \).
Ответ:
Найдите все значения \( \large a \: \), при каждом из которых наименьшее значение функции
\(f(x) = x-2|x|+|x^2-2(a+1)x+a^2+2a| \: \)
больше −4?
Найдите все значения \( \large a \: \), при каждом из которых наименьшее значение функции
\(f(x) = x-2|x|+|x^2-2(a+1)x+a^2+2a| \: \)
больше −4?
Заметим, что наименьшее значение функции больше −4, если все значения функции больше −4. Заданная функция непрерывна и на бесконечностях стремится к плюс бесконечности. Поэтому при любом значении параметра она достигает своего наименьшего значения. Тогда задачу можно переформулировать так: требуется найти все значения a, при каждом из которых неравенство
\(x-2|x|+|x^2-2(a+1)x+a^2+2a| \gt -4 \: \) (*)
выполняется при всех значениях \( \large x \: \).
Запишем неравенство в виде
\(|(x-a)(x-a-2)| \gt -4-x+2|x| \: \),
и построим графики левой и правой частей неравенства \( \large t(x) = |(x-a)(x-(a+2))| \: \) и \( \large s(x) = -4-x+2|x| \: \).
График функции \( \large t(x) \: \) — парабола с отраженной отрицательной частью, перемещающаяся по оси абсцисс, с корнями\( \large x=a \: \) и \( \large x=a+2) \: \)
График функции
\(s(x) = \begin{cases} -4-3x, при x \lt 0 \\ -4+x, при x\ge 0 \end{cases} \: \) — изображённая на рисунке ломаная (выделена синим цветом).
Для выполнения неравенства (*) необходимо, чтобы все точки графика \( \large y(x) = t(x) \: \) располагались выше графика \( \large y(x) = s(x) \: \) Граничные способы подходящего расположения подвижного графика \( \large y(x) = t(x) \: \) изображены на рисунке зелёным и красным цветом. Определим значения параметра для этих границ.
Левую границу найдём из условия касания прямой, задаваемой уравнением \( \large y=-3x-4 \: \) и параболы, задаваемой уравнением \( \large y=x^2-2(a+1)x+a^2+2a \: \). Они имеют единственную общую точку, а значит, уравнение
\(x^2-2(a+1)x+a^2+2a = -3x-4 \: \) имеет единственное решение. Запишем его в виде
\(x^2-(2a-1)x+a^2+2a+4 = 0 \: \) и найдем дискриминант полученного уравнения:
\(D=(2a-1)^2-4\cdot (a^2+2a+4) = -12a -15 \: \).
Он обращается в нуль при \( \large a=-1,25 \: \).
Правая граница достигается, если больший корень функции \( \large t(x) \: \) равен 4: \( \large a+2=4 \: \), откуда \( \large a=2 \: \).
Таким образом неравенство (*) выполняется при всех значениях \( \large x \: \), если \( \large -1,25 \lt a \lt 2 \: \).
\(-1,25 \lt a \lt 2 \: \).
Ответ: \(-1,25 \lt a \lt 2\).
Найдите все значения параметра при которых уравнение
\( (|x+2|+|x-a|)^2 - 3(|x+2|+|x-a|)+3a(5-3a) = 0 \: \)
имеет ровно два решения.
Найдите все значения параметра при которых уравнение
\( (|x+2|+|x-a|)^2 - 3(|x+2|+|x-a|)+3a(5-3a) = 0 \: \)
имеет ровно два решения.
Пусть \( \large t = |x+2|+|x-a| \: \) тогда исходное уравнение принимает вид:
\( t^2-5t+3a(5-3a) = 0 \Leftrightarrow \begin{cases} t=3a\\ t=5-3a\end{cases} \: \)
откуда
$$\left[\begin{gathered}|x+2| +|x - a| = 3a\\|x+2| +|x - a| = 5 - 3a\end{gathered}\right.$$Значит, решение исходного уравнения — это решение уравнений \( \large |x+2| +|x - a| = 3a \: \) или \( \large |x+2| +|x - a| = 5 - 3a \: \). Исследуем сколько решений имеет уравнение или \( \large |x+2| + |x - a| = b \: \) в зависимости от \( \large a \: \) и \( \large b \: \). Заметим, что слева стоит сумма модулей, то есть при \( \large b\lt 0 \: \) решений нет. Запишем уравнение в виде \( \large |x+2| = - |x - a| + b \: \) График левой части этого уравнения — график модуля с вершиной в точке \( \large (-2;0) \: \), график правой части — график модуля, отражённый относительно оси \( \large OX \: \), с вершиной в точке \( \large (a,b) \: \). Это уравнение будет иметь два решения, если одновременно прямая \( \large y=-x+a+b \: \) лежит правее (выше) прямой \( \large y=-x-2 \: \) и прямая \( \large y=x - a + b \: \) лежит левее (выше) прямой \( \large y=x+2x \: \) Это достигается условиями \( \large -x+a+b \gt -x-2 \: \) и \( \large x- a + b \lt x+2 \: \). Таким образом уравнение совокупности имеет два решения при условии:
$$\begin{cases}a+b \gt -2,\\a-b \lt -2,\\b \ge 0\end{cases}$$Если вершина \( \large (a,b) \: \) находится внутри части плоскости отсекаемой графиком \( \large y=|x+2| \: \), то уравнение имеет два решения, если прямые \( \large y=-x-2 \: \) и \( \large y=-x+a+b \: \) совпадают или прямые \( \large y=x+2 \: \) и \( \large y=x-a+b \: \) совпадают, то уравнение имеет бесконечно много решений, если вершина \( \large (a,b) \: \) совпадает с точкой \( \large (-2,0) \: \), то уравнение имеет одно решение.
Таким образом, исходное уравнение имеет ровно два решения, если одно из уравнений совокупности имеет два решения, а второе не имеет решений, либо если каждое из уравнений совокупности имеет два решения, но эти решения совпадают. Разберём каждый из этих случаев.
Первый случай. При \( \large a+b\lt -2 \: \) или \( \large a-b\gt -2 \: \), или \( \large b\lt 0 \: \) уравнение совокупности решений не имеет. Таким образом исходное уравнение имеет два решения, если первое уравнение имеет два решения, а второе — не имеет, либо наоборот. В случае, когда первое уравнение верно система условий имеет вид:
$$\begin{cases}\begin{cases}a+3a \gt -2,\\a-3a \lt -2,\\3a \ge 0\end{cases}\\\left[\begin{gathered}a+5-3a \lt -2\\a-5+3a \gt -2\\5-3a \lt 0\end{gathered}\right.\end{cases}В случае, когда второе уравнение верно система условий имеет вид:
Второй случай. Решения совпадут, если совпадают уравнения, то есть, если \( \large 3a = 5-3a \: \), откуда \( \large a=\frac{5}{6} \: \). При данном значении \( \large a \: \) оба уравнения прнимают вид:
\(|x+2|+|x-\frac{5}{6}| = \frac{5}{2} \: \)
Данное уравнение не имеет решений.
То есть исходное уравнение не имеет решений при \( \large a = \frac{5}{6} \: \).
Таким образом, уравнение имеет ровно два решения при \( \large a \in \left( - \infty; \frac{3}{4} \right) \cup (1;+\infty) \: \).
Ответ: \( \left( - \infty; \frac{3}{4} \right) \cup (1;+\infty) \)
