Найдите площадь ромба ABCD (в см2), если известно, что CD = 5, а BD = 8 см.
Найдите площадь ромба ABCD (в см2), если известно, что CD = 5, а BD = 8 см.
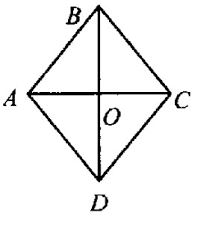
Так как диагонали ромба делятся пополам точкой пересечения, то
\(OD = \frac{8}{2}= 4 \: \)
Из \( \large \Delta DOC: \: \)
\(OC^2 = DC^2-OD^2 = \: \)
\(=5^2-4^2=9 \: \)
Т.е. ОС = 3. Следовательно, AC = 6.
Так как \( \large S = \frac{d_1\cdot d_2}{2} \: \), получаем ответ:
\(S = \frac{8\cdot 6}{2} = 24 \: \)
Ответ: 24

Сторона \( \large AB \: \) треугольника \( \large ABC \: \) c тупым углом \( \large C \: \) равна радиусу описанной около него окружности. Найдите угол \( \large C \: \). Ответ дайте в градусах.
Ответ: 150
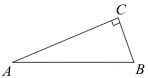
В треугольнике \( \large ABC \: \) угол \( \large C \: \) равен \( \large 90° \: \), \( \large tg A=\frac{33}{4\sqrt{33}} \: \),\( \large АС = 4 \: \). Найдите \( \large АВ \: \).
Имеем: \( \large AB =\frac{AC}{cosA} = \: \) \( \large \frac{AC}{\sqrt{\frac{1}{1+tg^2A}}} = \: \) \( \large \frac{4}{\sqrt{\frac{1}{1+\frac{33}{16}}}} \: \) \( \large =4\cdot \sqrt{\frac{49}{16}}=7 \: \)
Ответ: 7
Площадь параллелограмма \( \large ABCD \: \) равна 36. Точка \( \large E \: \) — середина стороны \( \large CD \: \). Найдите площадь трапеции \( \large ABDE \: \).
Проведём высоту параллелограмма из вершины \( \large B \: \) к продолжению стороны \( \large CD \: \). Площадь трапеции \( \large ABDE \: \) равна разности площадей параллелограмма \( \large ABCD \: \) и треугольника \( \large BCE \: \).
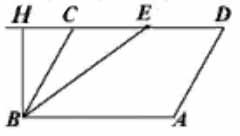
Имеем:
\(S_{ABCD} = CD\cdot BH \: \),
\(S_{BCE} = \frac{1}{2} \cdot CE\cdot BH = \frac{1}{2}\cdot \frac {1}{2} cdot CD\cdot BH = \frac{1}{4}\cdot S_{ABCD} = \frac{1}{4}\cdot 36 =9 \: \)
\(S_{ABED} = 36 -9 = 27 \: \)
Ответ: 27