На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: \( \large x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \: \). В скольких из этих точек производная функции f(x) отрицательна?
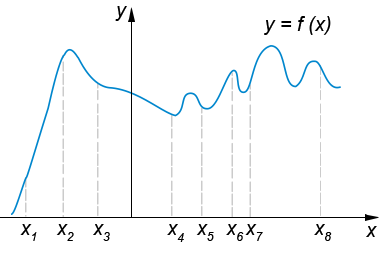
На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: \( \large x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \: \). В скольких из этих точек производная функции f(x) отрицательна?
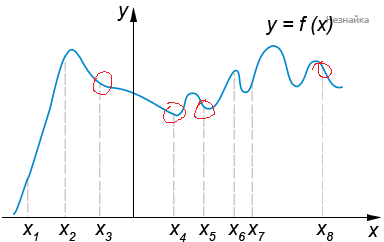
Производная функции отрицательна в тех точках, в которых график функции убывает: \( \large x_3, x_4, x_5, x_8 \: \)
Ответ: 4
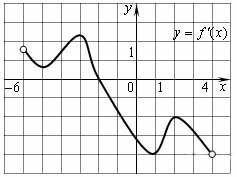
Функция \( \large y(x)=f(x) \: \) определена на промежутке \( \large (-6; -4) \: \). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция \( \large y=f(x) \: \) принимает наибольшее значение.
Ответ: -2
Материальная точка движется прямолинейно по закону \( \large x(t) = t^2 -13t+23 \: \) (где \( \large x \: \) — расстояние от точки отсчета в метрах, \( \large t \: \) — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна \( \large 3 м/с \: \)?
Найдем закон изменения скорости:
\(v(t)=x’(t)=2t-13 \: \) м/с
Чтобы найти, в какой момент времени \( \large t \: \) скорость была равна \( \large 3 м/с \: \), решим уравнение:
\(2t-13 = 3 \Leftrightarrow 2t=16 \Leftrightarrow t=8 c. \: \)
Ответ: 8
На рисунке изображены график функции \( \large y=f(x) \: \) и касательная к нему в точке с абсциссой \( \large x_0 \: \).
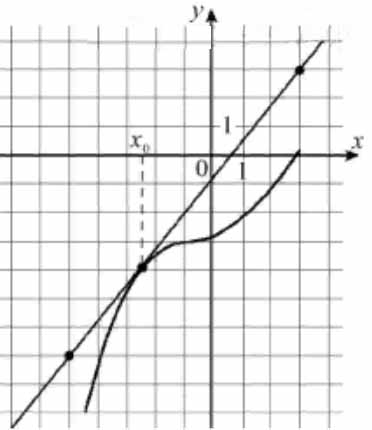
Найдите значение производной функции \( \large f(x) \: \) в точке \( \large x_0 \: \).
Пусть угол, который образует касательная с положительным направлением оси абсцисс, равен \( \large \alpha \: \), а угловой коэффициент касательной равен \( \large k \: \), т. е. \( \large k=tg\alpha \: \). Значение производной в точке касания равно угловому коэффициенту касательной, проведённой в этой точке, т.е. равно тангенсу угла \( \large \alpha \: \).
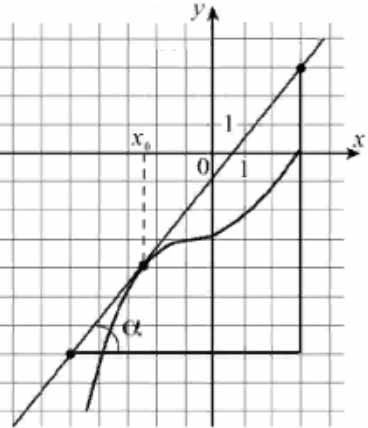
Из построенного прямоугольного треугольника находим: \( \large y'=tg\alpha =\frac{10}{8} = 1,25 \: \).
Ответ: 1,25