Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объём конуса ( в см3), в ответе укажите объем, делённый на \( \large pi \: \).
Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объём конуса ( в см3), в ответе укажите объем, делённый на \( \large pi \: \).
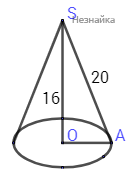
По теореме Пифагора находим OA из треугольника SAO: \( \large OA=\sqrt {AS^2-SO^2}= \: \)
\(=\sqrt {20^2-16^2}=12 \: \)
\(V=\frac13\cdot OS\cdot\pi\cdot AO^2= \: \)
\(=\frac13\cdot16\cdot\pi\cdot12^2=768\pi \: \)
Тогда в ответ: \( \large \frac{768\pi}\pi=768 \: \)
Ответ: 768
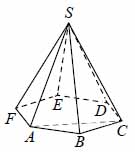
Найдите объём правильной шестиугольной пирамиды \( \large SABCDEF \: \), если объём треугольной пирамиды \( \large SABC \: \) равен 33.
Ответ: 198
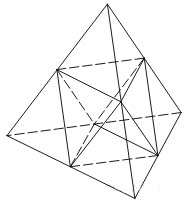
Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Объем данного многогранника равен разности объемов исходного тетраэдра \( \large V_0 \: \) и четырех тетраэдров, одни из вершин которых совпадают с вершинами исходного:
\(V=V_0-4\cdot \frac{1}{8}V_0 = \frac{1}{2}V_0 = 9,5 \: \)
Ответ: 9,5
В правильной четырёхугольной призме \( \large ABCDA_1B_1C_1D_1 \: \) известно, что \( \large DB_1 = 2C_1D_1 \: \). Найдите угол между диагоналями \( \large BD_1 \: \) и \( \large AC_1 \: \). Ответ дайте в градусах.
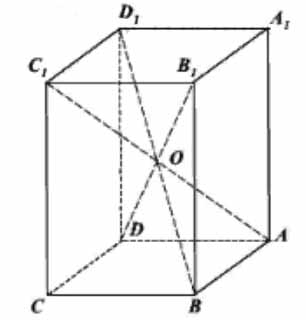
Пусть \( \large DB_1 \: \) и \( \large BD_1 \: \) пересекаются в точке \( \large O \: \). Так как правильная четырёхугольная призма является прямоугольным параллелепипедом, а диагонали прямоугольного параллелепипеда равны, то \( \large BD_1=DB_1=2C_1D \: \), то есть \( \large C_1D_1 = \frac{1}{2}BD_1 \: \). По свойству параллелепипеда получим также, что \( \large O \: \) – середина диагоналей призмы, т. е. \( \large OC_1 = OD_1 =\frac{1}{2}BD_1 \: \). Тогда \( \large C_1D_1 = \frac{1}{2}BD_1 = OD_1 = OC_1 \: \).
Значит, треугольник \( \large OC_1D_1 \: \) равносторонний, и угол \( \large C_1OD_1 =60^0 \: \).
Ответ: 60