Джинсы до распродажи стоили 1500 рублей. Катя купила джинсы во время распродажи со скидкой 20%. Сколько рублей Катя заплатила за джинсы?
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Джинсы до распродажи стоили 1500 рублей. Катя купила джинсы во время распродажи со скидкой 20%. Сколько рублей Катя заплатила за джинсы?
1500⋅(1-0,2)=1200 Ответ: 1200
Ответ: 1200
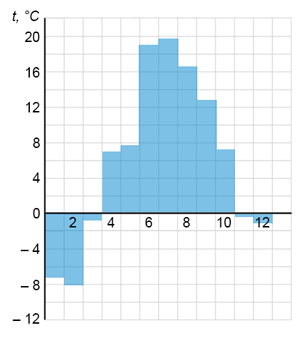
На диаграмме показана среднемесячная температура воздуха в Саратове за каждый месяц 2006 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 8 градусов Цельсия.
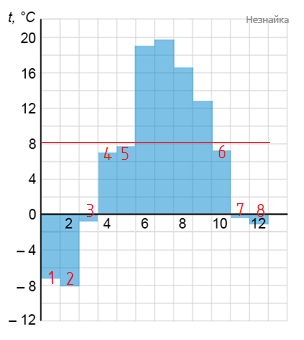
Ответ: 8
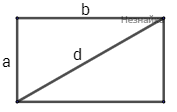
Периметр прямоугольника равен 17 см, а его площадь равна 15 см2. Найдите диагональ этого прямоугольника (в см).
Решите неравенство:
$$\begin{cases}P = (a+b) \cdot 2 = 17 \\S=a \cdot b=15\end{cases}$$Из первого уравнения \( \large a=8,5—b \: \). Подставляем во второе уравнение:\( (8,5-b)\cdot b =15 \: \)\( b^2-8,5\cdot b +15 =0 \: \)\( 2b^2-17\cdot b +30 =0 \: \)\( D=17^2-4\cdot 2\cdot 30 =49 \: \)\( b_1=\frac{17+\sqrt{49}}{2\cdot2}=6 \: \)\( a=8,5—6=2,5 \: \)\(d=\sqrt{a^2+b^2}= \: \) \(=\sqrt{2,5^2+6^2}=6,5 \: \)Ответ: 6,5
На мероприятие было закуплено 13 синих, 11 красных, 6 жёлтых и 20 белых футболок. Какова вероятность того, что Саше достанется красная футболка?
\(\frac{11}{13+11+6+20}=0,22 \: \)
Ответ: 0,22
Решите уравнение:
\(\sqrt{\frac{2x+7}4}=2 \: \)
\(\sqrt{\frac{2x+7}4}=2 \: \)
\(\frac{2x+7}4=4 \: \)
\(2x+7=16 \: \)
\(2x=9 \: \)
\(x=4,5 \: \)
Ответ: 4,5
Найдите площадь ромба ABCD (в см2), если известно, что CD = 5, а BD = 8 см.
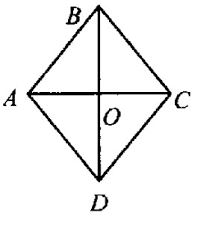
Так как диагонали ромба делятся пополам точкой пересечения, то
\(OD = \frac{8}{2}= 4 \: \)
Из \( \large \Delta DOC: \: \)
\(OC^2 = DC^2-OD^2 = \: \)
\(=5^2-4^2=9 \: \)
Т.е. ОС = 3. Следовательно, AC = 6.
Так как \( \large S = \frac{d_1\cdot d_2}{2} \: \), получаем ответ:
\(S = \frac{8\cdot 6}{2} = 24 \: \)
Ответ: 24
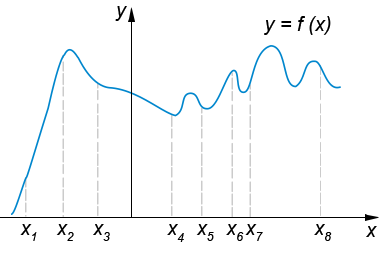
На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: \( \large x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \: \). В скольких из этих точек производная функции f(x) отрицательна?
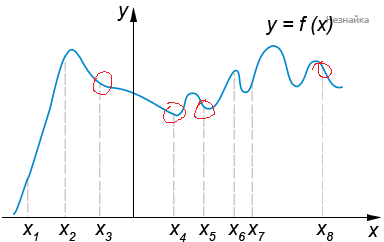
Производная функции отрицательна в тех точках, в которых график функции убывает: \( \large x_3, x_4, x_5, x_8 \: \)
Ответ: 4
Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объём конуса ( в см3), в ответе укажите объем, делённый на \( \large pi \: \).
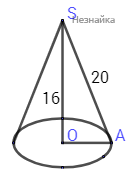
По теореме Пифагора находим OA из треугольника SAO: \( \large OA=\sqrt {AS^2-SO^2}= \: \)
\(=\sqrt {20^2-16^2}=12 \: \)
\(V=\frac13\cdot OS\cdot\pi\cdot AO^2= \: \)
\(=\frac13\cdot16\cdot\pi\cdot12^2=768\pi \: \)
Тогда в ответ: \( \large \frac{768\pi}\pi=768 \: \)
Ответ: 768
Найдите значение выражения: \( \large \frac{log_\frac1427}{log_43} \: \)
\(\frac{log_\frac1427}{log_43}=\frac{log_427}{log_4\frac{1}{4}\cdot log_43}=\frac{log_43^3}{(-1)\cdot log_43}= \: \)
\(=\frac{3log_43}{(-1)log_43}=-3 \: \)
Ответ: -3
На нагревание 5 кг воды потребовалось количество теплоты, равное 1 890 000 Дж, которое можно рассчитать по формуле \( \large Q=cm(t_2-t_1) \: \), где Q — количество теплоты, c — удельная теплоемкость вещества, m — масса вещества, t1 — начальная температура, t2 — конечная температура вещества. До какой температуры (в °С) нагрелась вода, если удельная теплоемкость воды равна \( \large 4200\frac{Дж}{кг\cdot^\circ С} \: \), а ее начальная температура 1°С?
\(Q=cm(t_2-t_1) \: \)
1 890 000 = 4200⋅5⋅(t2—1)
t2—1 = 90
t2 = 91
Ответ: 91
Из города А в город В в одно и то же время выехали два автомобиля. Расстояние между городами 350 км. Второй автомобиль проехал с постоянной скоростью и без остановок весь путь. Первый автомобиль проехал первую половину пути, затем сделал остановку на 1 час, после чего продолжил путь с прежней скоростью. В итоге первый автомобиль прибыл в город В на 3 часа позже, чем второй. Найдите скорость второго автомобиля, если известно, что она больше скорости первого на 20 км/ч. Ответ дайте в км/ч.
Пусть Х км/ч скорость 2-го автомобилиста, тогда скорость 1-го — (Х—20) км/ч. Второй автомобилист проехал путь за \( \large \frac{350}Х \: \) часов, а первый за \( \large 1+\frac{350}{Х-20} \: \). Первый прибыл в город позже второго на \( \large \frac{350}{Х-20}+1-\frac{350}Х \: \) часов, а по условию на 3. Получили уравнение:
\(\frac{350}{Х-20}+1-\frac{350}Х=3 \: \)
\(Х^2-20Х-3500=0 \: \)
\(D=\left(-20\right)^2-4\cdot3500=14400 \: \)
Возьмем только положительный корень: \( \large Х=\frac{20+\sqrt{14400}}2=70 \: \). Т.е. 70 км/ч скорость второго автомобиля
Ответ: 70
Найдите точку минимума функции \( \large y=(x-5)e^{x+2} \: \)
Найдем производную и точки, в которых она равна 0 или не существует, разобьем ими область определения функции на отрезки и определим знаки производной на них. Переход знака производной с отрицательного значения в положительное будет точкой минимума \( \large y=(x-5)e^{x+2} \: \)
\(y'=\left(\left(x-5\right)e^{x+2}\right)'= \: \)
\(e^{x+2}+(x-5)e^{x+2}=(x-4)e^{x+2} \: \)
y'=0 при x=4. При х<4 производная отрицательная, при x>4 производная положительная, значит x=4 — точка минимума
Ответ: 4
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
Дано уравнение \( \large \sqrt x=\sqrt{\left[x\right]}+\sqrt{\left\{x\right\}} \: \), , где [a] — целая часть числа а, т.е. наибольшее целое число, не превосходящее а; {a} — дробная часть числа а, т.е. {a} = а - [a].
а) Решите уравнение
б) Найдите его корни, принадлежащие отрезку \( \large \left[tg\frac\pi{12};\;tg\frac{5\pi}{12}\right] \: \)
а) Преобразуем уравнение:\( \large \sqrt x=\sqrt{\left[x\right]}+\sqrt{x-\left[x\right]} \: \).
Так как левая и правая части уравнения неотрицательны, возведем в квадрат обе части уравнения. Получим:
\(x=\left[x\right]+2\sqrt{\left[x\right]x-\left[x\right]^2}+x-\left[x\right] \: \)
\(2\sqrt{\left[x\right]x-\left[x\right]^2}=0 \: \)
\(\left[x\right]x-\left[x\right]^2=0 \: \)
\(\left[x\right](x-\left[x\right])=0 \: \)
Имеем два случая:
1 случай:
\(\left[x\right]=0 \: \)
т.е. целая часть равна 0. Имеем
\(0\leq x<1 \: \)
2 случай:
\(x-\left[x\right]=0 \: \)
\(x=\left[x\right] \: \)
т.е. число-целое,дробной части нет, \( \large x\in N \: \).
б) Преобразуем tg:
\(tg\frac\pi{12}=\sqrt{\frac{1-cos\frac\pi6}{1+cos\frac\pi6}}=\sqrt{\frac{1-\frac{\sqrt3}2}{1+\frac{\sqrt3}2}}= \: \)
\(\sqrt{\frac{(1-\frac{\sqrt3}2)^2}{1-\frac34}}=\frac{1-\frac{\sqrt3}2}{\frac12}= \: \)
\(=2(1-\frac{\sqrt3}2)\approx0.3 \: \)
\(tg\frac{5\pi}{12}=\sqrt{\frac{1-cos\frac{5\pi}6}{1+cos\frac{5\pi}6}}=\sqrt{\frac{1+cos\frac\pi6}{1-cos\frac\pi6}}= \: \)
\(=\frac{1+\frac{\sqrt3}2}{\frac12}=2(1+\frac{\sqrt3}2)\approx3.7 \: \)
Имеем,что в промежуток \( \large 0\leq x<1 \: \) входит \( \large \lbrack tg\frac\pi{12};1) \: \).
В промежуток \( \large x\in N \: \) входит x=1; 2; 3.
Ответ а) \( \large 0\leq x<1 \: \) или \( \large x\in N \: \)
б)\( \large \left[tg\frac\pi{12};\;1\right]\cup\left\{2;3\right\} \: \)
Ответ: а) \(0\leq x<1\) или \(x\in N\) б)\(\left[tg\frac\pi{12};\;1\right]\cup\left\{2;3\right\}\)
В пирамиде SABC угол ASB равен 60°, а углы BSC и CSA - по 45°.
а) Докажите, что плоскости BSC и ASC перпендикулярны.
б) Найдите радиус сферы вписанной в пирамиду SABC, если известно, что SA=SB=2, \( \large SC=2\sqrt 2 \: \).
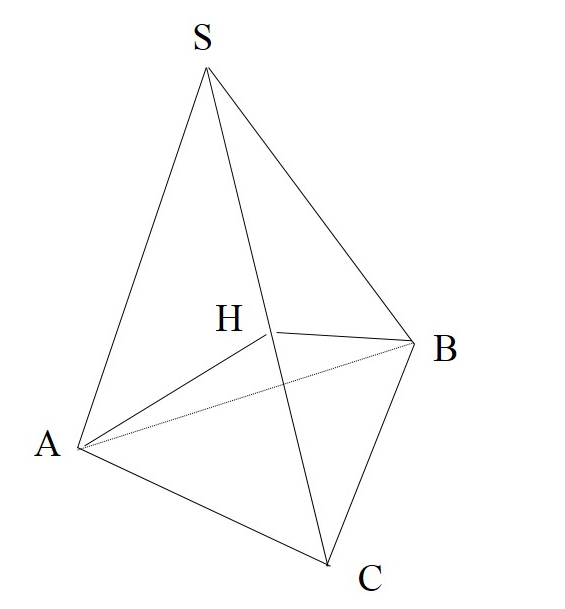
Дано: SABC -пирамида, \( \large \angle ASB=60^\circ, \angle BSC=\angle CSA \: \)\( \large =45^\circ \: \), \( \large r \: \) - радиус вписанной в пирамиду сферы, \( \large SA=SB=2, SC=2\sqrt 2 \: \).
а) Доказать, \( \large (BSC)\bot (ASC) \: \)
б) Найти \( \large r \: \)
а) Т.к. AS=SB, то треугольник \( \large ASB \: \)-равнобедренный. Следовательно, \( \large \angle SAB=\angle SBA=\frac{180^\circ-60^\circ}2=60^\circ \: \). Т.к. все углы треугольника равны 60,то треугольник ASB-равносторонний, т.е. \( \large AC=CB=AB \: \).
\(\bigtriangleup ASC=\bigtriangleup BSC \: \) (по первому признаку равенства треугольников, т.к. AS=CB, \(\angle ASC=\angle CSB \: \), SC-общая). Следовательно, AC=BC.
\(\bigtriangleup SCB: \: \) по теореме косинусов имеем, что
\(BC^2=SC^2+BS^2 \: \) \(-2\cdot SC\cdot BS\cdot cos(\angle CSB) \: \)
\(BC^2=8+4-2\cdot2\sqrt2\cdot 2\cdot\frac{\sqrt2}2\Rightarrow \: \) \(BC^2=4\Rightarrow BC=2 \: \)
т.е. BC=AC=2,SB=AS=2. Следовательно, \( \large \bigtriangleup ASC,\bigtriangleup SCB \: \) - равнобедренные \( \large \Rightarrow\angle SCA=\angle SCB=45^\circ \: \) \( \large \Rightarrow\;\angle SAC=\angle SBC=90^\circ \: \)
Проведем \( \large BH\bot SC \: \), то есть высоту в треугольнике \( \large ASC \: \). Имеем, что AH-высота треугольника BSC. т.е. \( \large BH\bot SC AH\bot SC \: \). Имеем по определению двугранный угол AHB,причем в треугольнике AKB \( \large AH=HB=\sqrt 2 \: \). По теореме косинусов найдем \( \large \angle AHB \: \) и получим,что \( \large \angle AHB=90^\circ \: \). Следовательно, и двугранный угол \( \large \angle AHB=90^\circ \: \), т.е. искомые плоскости перпендикулярны, что и требовалось доказать.
б) Чтобы найти радиус вписанной сферы, воспользуемся следующей формулой: \( \large r=\frac{V_{пир}}{S_{полн}} \: \)
Найдем объем пирамиды:
\(V_{пир}=\frac13S_{SBC}\times AH= \: \) \(\frac13\cdot (\frac12\cdot2\cdot 2) \: \) \(\times\sqrt2=\frac{2\sqrt2}3 \: \)
Найдем площадь всей поверхности пирамиды:
\(S_{полн}=2\times S_{ASB}+2\times S_{ASC}= \: \) \(2\cdot\frac{4\sqrt3}4+2\cdot\frac12\cdot2\cdot2 \: \) \(=2\sqrt3+4 \: \)
\(r=\frac{3\cdot2\sqrt2}{3\cdot(2\sqrt3+4)}=\frac{\sqrt2(\sqrt3-2)}{3-4}= \: \) \(\sqrt8-\sqrt6 \: \)
Ответ: \( \large \sqrt8-\sqrt6 \: \)
Ответ: б) \(\sqrt8-\sqrt6\)
Решите неравенство \( \large 4^x+\frac{16}{x^2}\geq5\cdot\frac{2^{x+1}}x \: \)
\(4^x+\frac{16}{x^2}\geq5\times\frac{2^{x+1}}x \: \)
\(2^{2x}+\frac{16}{x^2}\geq10\times\frac{2^x}x \: \)
Домножим обе части на \( \large \frac x{2^x} \: \). Получим 2 случая:
1) \( \large 2^x\times x+\frac{16}{2^x\times x}\geq10 \: \)
Пусть \( \large y=2^x\times x \: \). Тогда \( \large y+\frac{16}y\geq10 \: \)
\(\frac{y^2+16-10y}y\geq0 \: \)
Нули числителя: \( \large y^2+16-10y=0 \: \)
\(D=100-16\cdot4=100-64=36 \: \). Откуда \(y_1=8, y_2=2 \: \).
Получаем тогда:
\(\frac{(y-8)(y-2)}y\geq0 \: \)
Решая методом интервалов, получим: \( \large (0;1]\bigcup[2;+\infty) \: \)
2) \( \large x<0 \: \) \( \large \frac{y^2+16-10y}y\leq0 \: \) или \( \large \frac{(y-8)(y-2)y}y\leq0 \: \).
Решая методом интервала с учетом: \( \large x<0 \: \) получим, \( \large (-\infty;0) \: \).
Окончательный ответ: \( \large (0;1]\bigcup[2;+\infty)\bigcup (-\infty;0) \: \)
Ответ: \((0;1]\bigcup[2;+\infty)\bigcup (-\infty;0)\)
а) На координатной плоскости \( \large ОXY \: \) изобразите фигуру, заданную неравенством \( \large \log_{x^2+y^2}\left(x+y\right)>1 \: \)
б) Найдите площадь полученной фигуры.
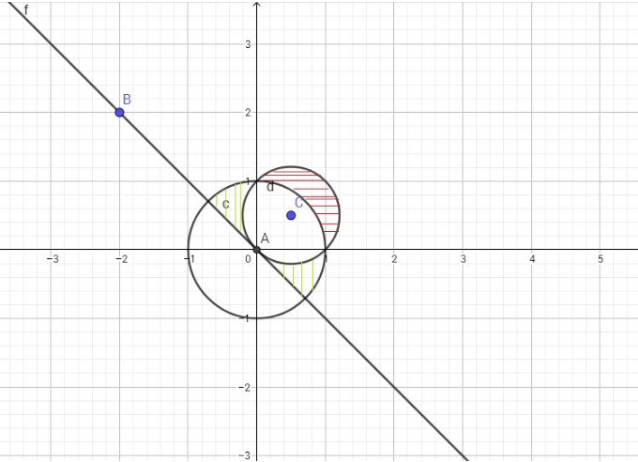
ОДЗ:
\(x+y>0 \: \), \(y>-x \: \)
\(x^2+y^2>0 \: \) всегда, кроме x=0; y=0
\(x^2+y^2\neq1 \: \). Окружность с центром \(О_1(0;0) \: \) и радиусом \(R=1 \: \). Изображаем пунктиром.
Преобразуем правую часть уравнения: \( \large 1=log_{x^2+y^2}(x^2+y^2) \: \)
Тогда получим:
\(log_{x^2+y^2}(x+y)> \: \)\(log_{x^2+y^2}(x^2+y^2) \: \)
1 сл: \( \large x^2+y^2>1 \: \)
\(\frac{x+y}{x^2+y^2}>1 \: \)
\(\frac{x+y-x^2-y^2}{x^2+y^2}>0 \: \)
\(\frac{-x-y+x^2+y^2}{x^2+y^2}<0 \: \)
\(-x-y+x^2+y^2<0 \: \)
\(\left(x-\frac12\right)^2+\left(y-\frac12\right)^2>\frac12 \: \)
Окружность с центром в точке (1/2;1/2) и радиусом \( \large R=\frac1{\sqrt2} \: \) при \( \large x^2+y^2>1 \: \)
2 сл. \( \large 0 < x^2+y^2 < 1 \: \)
\(\frac{x+y}{x^2+y^2}<1 \: \)
\(\frac{x+y-x^2-y^2}{x^2+y^2}<0 \: \)
\(\frac{-x-y+x^2+y^2}{x^2+y^2}>0 \: \)
\(-x-y+x^2+y^2>0 \: \)
\(\left(x-\frac12\right)^2+\left(y-\frac12\right)^2>\frac12 \: \)
Окружность с центром в точке (1/2;1/2) и радиусом \( \large R=\frac1{\sqrt2} \: \) при \( \large 0 < x^2+y^2 < 1 \: \) (см. рисунок)
Найдем площадь полученной фигуры:
\(S_{green}=\frac12S_{бол\;окр}-(\frac12S_{мал\;окр}+ \: \)
\((\frac14S_{бол}-S_{прям\;треуг}) \: \) \(=\frac\pi2-(\frac\pi4+(\frac\pi4-\frac12)=\frac12 \: \)
\(S_{red}=\frac12S_{мал\;окр}- \: \) \((\frac14S_{бол}- \: \) \(S_{прям\;треуг})=\frac\pi4- \: \) \((\frac\pi4-\frac12)= \: \) \(\frac12 \: \)
\(S_{полн}=S_{green}+S_{red}=\frac12+\frac12 \: \) \(=1 \: \)
Ответ: 1
Накануне Нового года Деды Морозы раскладывали равными количествами конфеты в подарочные пакеты, а эти пакеты складывали в мешки, по 2 пакета в один мешок. Те же самые конфеты они могли разложить в пакеты так, что в каждом из них было бы на 5 конфет меньше, чем раньше, но тогда в каждом мешке стало бы лежать по 3 пакета, а мешков при этом потребовалось бы на 2 меньше. Какое наибольшее количество конфет могли раскладывать Деды Морозы?
Пусть x- количество конфет в одном пакете, а y- количество мешков.Тогда в первом случае 2xy, а во втором случае-3(x−5)(y−2). Так как было одинаковое количество конфет, то получим уравнение: 2xy=3(x−5)(y−2). Преобразуем: (x−15)(y−6)=60. Т.е множители должны быть натуральными числами и в произведении давать число 60. При переборе должны получить числа 1 и 60, 2 и 30, 3 и 20 и тд. После перебора, получим,что максимальное xy получаем при значениях множителей 1 и 60, то есть x=16, y=66. т.е. получаем общее количество конфет 2xy=2*16*66=2112.
Ответ: 2112
Для каждого значения параметра \( \large a \: \) найдите наибольшее значение функции \( \large f\left(x\right)=\left(\left|x\right|-6\right)\cdot x^2+ \: \) \( \large 3\left|x\right|\cdot\left(3-a^2\right)+ \: \) \( \large 6ax \: \) на отрезке \( \large [-3; 3] \: \)
Имеем два случая: 1) \( \large x\geq0 \: \) 2) \( \large x<0 \: \),
1 случай: \( \large x\geq0 \: \). Преобразуем функцию:
\(f(x)=x^3-6x^2+ \: \) \((9+6a-3a^2)x \: \)
Найдем производную функции:
\(f'(x)=3x^2-12x+ \: \) \((9+6a-3a^2) \: \)
\(f'(x)=0 \: \)
\(x^2-4x+3+2a-a^2=0 \: \)
\(D=16-4(3+2a-a^2)= \: \) \(4(a-1)^2 \: \)
\( x_1=3-a \: \), \(x_2=1+a \: \)
Определим знак производной:
1) \( \large 0\lt a\lt 1 \: \); \( \large 1\lt a+1\lt 2 \: \); \( \large 2\lt 3-a \lt 3 \: \)
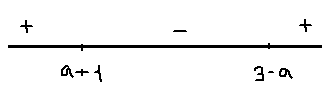
\(x=a+1 \: \) - точка максимума;
\(fmax=f(a+1)= \: \) \(-2(a+1)(a^2-a-2) \: \)
2) \( \large 1\lt a \lt 2 \: \); \( \large 2 \lt a+1 \lt 3 \: \);\( \large 1\lt3-a\lt2 \: \)
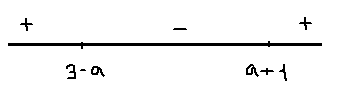
\(x=3-a \: \) - точка максимума
\(fmax=f(3-a)= \: \) \(2(3-a)(6-a) \: \)
3) \( \large 2 \lt a \lt 3 \: \); \( \large 3\lt a+1\lt 4 \: \); \( \large 0 \lt 3-a\lt 1 \: \)
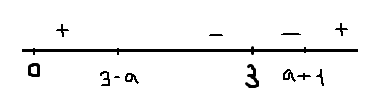
\(x=a+1 \: \) не принадлежит отрезку \(x=3-a \: \)- точка максимума
4) \( \large a>3 \: \)
\(x=a+1, x=3-a \: \), не принадлежат отрезку значений \(x \: \), т.к. т.к. функция убывает, то \(fmax=f(0) \: \)
2 случай: \( \large x\lt 0 \: \). Преобразуем функцию:
\(f(x)=-x^3-6x^2+ \: \) \((-9+6a+3a^2)x \: \)
Найдем производную функции:
\(f'(x)=-3x^2-12x+ \: \) \((-9+6a+3a^2) \: \)
\(f'(x)=0 \: \)
\(x^2+4x+3-2a-a^2=0 \: \)
\(D=16-4(3-2a-a^2)= \: \) \(4(a+1)^2 \: \)
\(x_1=-3-a \: \), \(x_2=-1+a \: \)
Определим знак производной:
1) \( \large -1\lt a\lt 0 \: \);\( \large -3\lt -3-a\lt -2 \: \); \( \large -2\lt a-1\lt -1 \: \)
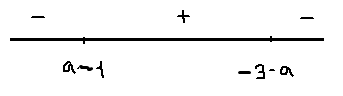
\(x=a-1 \: \) - точка максимума;
\(fmax=f(a-1)= \: \) \(-2(a-1)(a^2+2a+2) \: \)
2) \( \large -2\lt a\lt -1 \: \); \( \large -3\lt a-1\lt -2 \: \);\( \large -2\lt -3-a\lt -1 \: \)
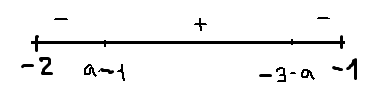
\(x=-3-a \: \) - точка максимума
\(fmax=f(-3-a)= \: \) \(2a(-3-a)(a+3) \: \)
3) \( \large -3 \lt a\lt -2 \: \); \( \large -4\lt a1\lt -3 \: \);
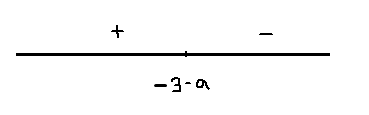
\(x=-3-a \: \) точка максимума
\(fmax=f(-3-a)= \: \) \(2a(-3-a)(a+3) \: \)
4) \( \large a\lt -3 \: \); \( \large a-10 \: \)
т.к. функция убывает, то \( \large fmax=f(-3)=-9a^2-18a \: \)
Ответ:
при \( \large a\le -3 \: \), \( \large f_{max}=–9a^2–18a \: \);
при \( \large -3\lt a\le-1 \: \), \( \large f_{max}=-2a(a+3)^2 \: \);
при \( \large -1\lt a\le 0, \: \) \( \large f_{max}=2\cdot (a–1) \cdot (a^2+2a+2) \: \);
при \( \large 0\lt a\le1 \: \), \( \large f_{max}=(a+1) \cdot (–2a^2+2a+4)) \: \);
при \( \large 1\lt a\le 3 \: \), \( \large f_{max}=2\cdot (3–a) \cdot (6–a) \: \);
при \( \large a\gt 3 \: \), \( \large f_{max}=0 \: \).
Ответ:
Чук и Гек поочередно извлекают из трех ящиков шары. Своим ходом каждый может взять из любого ящика (но только из одного) любое количество шаров. Выигрывает тот, кто заберет последний шар. Кто из мальчиков может обеспечить себе победу независимо от игры соперника, если количество шаров в ящиках равно:
A) 8, 9 и 9;
Б) 1, 2 и 3;
B) 8, 9 и 10?
Существует несколько исходов игры, которые гарантируют победу первому участнику,это (вне зависимости от последовательности ящиков): 1 0 0,N 1 1,N 1 0, N 0 0 , где N- любое натуральное число,и гарантированное проигрышные ситуации-1 1 0, 2 2 0. Исходя из этого будет идти решение задачи.
А) Чтобы выиграл Чук, нам необходимо привести Гека к варианту 110. Если Чук возьмет 8 шаров из первого ящика, то есть сравняет количество шаров только во втором и третьем, тогда Чуку остается каждый раз уравнивать количество шаров до того момента,пока не станет вариант 1 1 0. т.е. выиграет Чук
Б) Исходя из базовых ситуаций найдем ситуации выигрыша: M 2 0 (M>=3), 2 2 1,3 2 0 (их можно привести к ситуации проигрыша , то есть к 2 2 0). Ситуацию 1 2 3 возможно привести только к выигрышу,следовательно ,она проигрышна для первого, т.е. выиграет Гек.
В) В таком варианте Чук сможет выиграть, если будет сравнивать две цифры каждый раз, в конце дойдет до варианта 011 и победит. Это возможно в любом случае
Ответ: А) Чук;Б) Гек;В) Чук