Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Ответ: 15
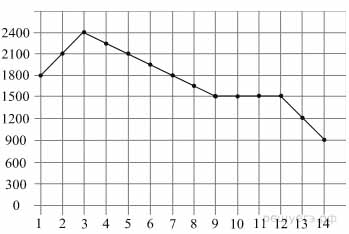
На рисунке жирными точками показано изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. Для наглядности жирные точки на рисунке соединены линией. По горизонтали указываются числа месяца, по вертикали — стоимость акции в рублях. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
Ответ: 4500
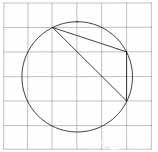
На клетчатой бумаге с размером клетки \( \large \sqrt5 \times \sqrt 5 \: \) изображён треугольник. Найдите радиус его описанной окружности.
Ответ: 5
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Ответ: 0,02
Решите уравнение \( \large \frac{13x}{2x^2-7}=1 \: \). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Ответ: -0,5

Сторона \( \large AB \: \) треугольника \( \large ABC \: \) c тупым углом \( \large C \: \) равна радиусу описанной около него окружности. Найдите угол \( \large C \: \). Ответ дайте в градусах.
Ответ: 150
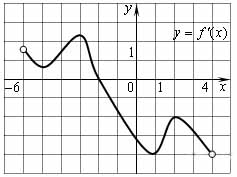
Функция \( \large y(x)=f(x) \: \) определена на промежутке \( \large (-6; -4) \: \). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция \( \large y=f(x) \: \) принимает наибольшее значение.
Ответ: -2
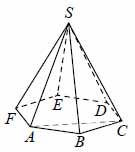
Найдите объём правильной шестиугольной пирамиды \( \large SABCDEF \: \), если объём треугольной пирамиды \( \large SABC \: \) равен 33.
Ответ: 198
Найдите значение выражения \( \large log_a(ab^3) \: \), если \( \large log_ba=\frac17 \: \)
Ответ: 22
При нормальном падении света с длиной волны \( \large \lambda = 400 \: \) нм на дифракционную решeтку с периодом \( \large d \: \) нм наблюдают серию дифракционных максимумов. При этом угол \( \large \varphi \: \) (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума \( \large k \: \) связаны соотношением \( \large dsin\varphi =k\lambda \: \). Под каким минимальным углом \( \large \varphi \: \) (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1600 нм?
Ответ: 30
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Ответ: 8,4
а) Решите уравнение \( \large 8sin^2\left( \frac{7\pi}{12}+x\right) -2\sqrt 3 cos2x=5 \: \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( \large \left[ -\frac{7\pi}{2};-\frac{5\pi}{2}\right] \: \).
а) Заметим, что \( \large sin\left(\frac{7\pi}{12}+x\right) = \: \) \( \large sin\left( \frac{\pi}{2}+\frac{\pi}{12}+x\right) = \: \) \( \large cos\left(\frac{\pi}{12}+x\right) \: \).
Преобразуем уравнение:
\(8sin^2\left(\frac{7\pi}{12}+x\right)-2\sqrt 3 cos 2x=5 \: \) \(\Rightarrow \: \) \((8cos^2\left(\frac{\pi}{12}+x\right)-2\sqrt 3 cos 2x=5 \: \) \(\Rightarrow \: \) \(4\left(2cos^2\left(\frac{\pi}{12}+x\right)-1\right)+4-2\sqrt 3cos2x \: \) \(\Rightarrow \: \) \(4cos\left(\frac{\pi}{6}+2x\right)+4-2\sqrt3 cos2x=5 \: \) \(\Rightarrow \: \) \(4\left(\frac{\sqrt3}{2}cos2x-\frac{1}{2}sin2x\right) \: \)+4-2\sqrt3 cos2x=5 \: \) \(\Rightarrow \: \) \(2\sqrt3cos2x-2sin2x-2\sqrt3cos2x=1 \: \) \(\Rightarrow \: \) \(2sin2x = -1 \: \) \(\Rightarrow \: \) \(sin2x = -\frac{1}{2} \: \) \(\Rightarrow \: \) \( \begin{cases} 2x = -\frac{\pi}{6}+2\pi k \\2x = -\frac{5\pi}{6}+2\pi k \end{cases} \: \) \(\Rightarrow \: \) \( \begin{cases} x = -\frac{\pi}{12}+\pi k \\x = -\frac{5\pi}{12}+\pi k, k\in Z \end{cases} \: \)
б) С помощью числовой окружности (см. рис.)
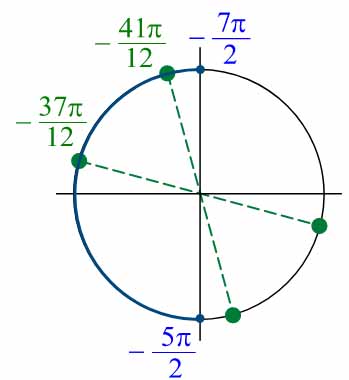
отберём корни, принадлежащие отрезку \( \large \left[ -\frac{7\pi}{2};-\frac{5\pi}{2}\right] \: \). Получим числа \( \large -\frac{41\pi}{12};-\frac{37\pi}{12} \: \).
Ответ: а) \(x = -\frac{\pi}{12}+\pi k\), \(x = -\frac{5\pi}{12}+\pi k, k\in Z\) б) \(-\frac{41\pi}{12};-\frac{37\pi}{12}\)
Дана пирамида \( \large SABC \: \), в которой \( \large SC=SB=AB=AC=\sqrt {17} \: \), \( \large SA = BC =2\sqrt5 \: \).
а) Докажите, что ребро \( \large SA \: \) перпендикулярно ребру \( \large BC \: \).
б) Найдите расстояние между ребрами \( \large BC \: \) и \( \large SA \: \).
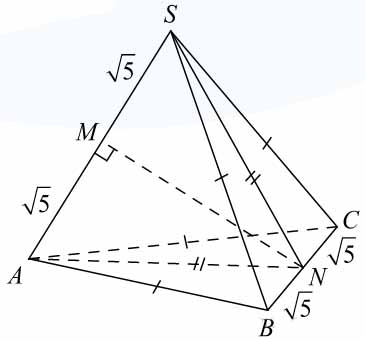
а) Заметим, что треугольники \( \large SBC \: \) и \( \large АВС \: \) равны по трем сторонам. Они являются равнобедренными и имеют общее основание. Проведем медианы \( \large SN \: \) и \( \large AN \: \) к этому основанию. Они попадут в одну точку точку \( \large N \: \), которая является серединой \( \large ВС \: \) и будут являться высотами данных треугольников. Тем самым, прямая \( \large BC \: \) перпендикулярна двум пересекающимся прямым плоскости \( \large ASN \: \), а значит, и всей этой плоскости. Но тогда прямая \( \large ВС \: \) перпендикулярна любой прямой плоскости \( \large ASN \: \). В частности, перпендикулярна прямой \( \large SA \: \).
б)
Построим высоту \( \large NМ \: \) треугольника \( \large ASN \: \). Заметим, что \( \large NМ \: \) является общим перпендикуляром прямых \( \large AS \: \) (по построению) и \( \large ВС \: \), поскольку \( \large NМ \: \) лежит в плоскости \( \large ASN \: \). Тогда длина \( \large NМ \: \) и есть искомое расстояние между скрещивающимися прямыми \( \large AS \: \) и \( \large ВС \: \).
Заметим, что \( \large SN = AN = \sqrt{17-5}=\sqrt{12} \: \). Тогда треугольник \( \large SNA \: \) равнобедренный, его высота \( \large NМ \: \) является также медианой, а тогда из прямоугольного треугольника \( \large АМN \: \) находим: \( \large NM=\sqrt{AN^2-AM^2} = \sqrt{12-5} \: \) \( \large = \sqrt7 \: \).
Ответ: б) \(\sqrt7\)
Решите неравенство: \( \large \left(\frac{10}{5x-21}+\frac{5x-21}{10}\right)^2 \le \frac{25}{4} \: \).
Сделав замену \( \large t=\frac{5x-21}{10} \: \), получаем:
\(\left(\frac1t+t\right)^2\le \frac{25}{4} \: \) \(\Rightarrow \: \) \(-\frac{5}{2} \le \frac{1}{t}+ t \le \frac{5}{2} \: \) \(\Rightarrow \: \) \(-5\le \frac{2t^2+2}{t}\le 5 \: \) \(\Rightarrow \: \) \(\begin{cases} \frac{2t^2-5t+2}{t} \le 0, \\ \frac{2t^2 + 5t+2}{t} \ge 0 \end{cases} \: \) \(\Rightarrow \: \) \(\begin{cases} \frac{2(t-2)(t-\frac12)}{t} \le 0, \\ \frac{2(t +2)(t + \frac12)}{t} \ge 0 \end{cases} \: \) \(\Rightarrow \: \) \(\left[\begin{array}{l}-2 \le t \le -\frac12\\\frac12 \le t \le 2\end{array}\right. \: \)/
Возвращаясь к исходной переменной, получаем:
\(\left[\begin{array}{l}5\le5x-21\le20\\-20\le 5x-21\le -5 \end{array}\right. \: \) \(\Rightarrow \: \) \(\left[\begin{array}{l}\frac{26}{5}\le x \le \frac{41}{5},\\ \frac15 \le x \le \frac{16}{5} \end{array}\right. \: \)
Ответ: \(\left[ \frac15; \frac{16}{5}\right] \cup \left[\frac{26}{5};\frac{41}{5}\right]\)
Дана трапеция \( \large ABCD \: \) с основаниями \( \large BC \: \) и \( \large AD \: \). Точки \( \large M \: \) и \( \large N \: \) являются серединами сторон \( \large AB \: \) и\( \large CD \: \) соответственно. Окружность, проходящая через точки \( \large B \: \) и \( \large С \: \), пересекает отрезки \( \large BM \: \) и \( \large CN \: \) в точках \( \large P \: \) и \( \large Q \: \) (отличных от концов отрезков).
а) Докажите, что точки \( \large M \: \), \( \large N \: \), \( \large P \: \) и \( \large Q \: \) лежат на одной окружности.
б) Найдите \( \large QN \: \), если отрезки \( \large DP \: \) и \( \large PC \: \) перпендикулярны, \( \large AB = 21 \: \), \( \large BC = 4 \: \), \( \large CD = 20 \: \), \( \large AD = 17 \: \).
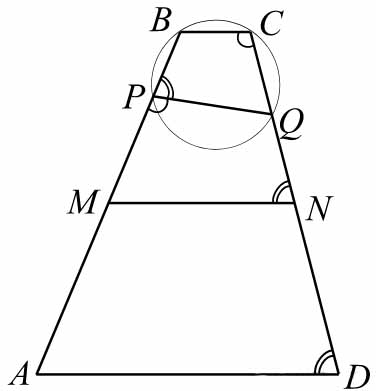
a) По условию, четырёхугольник \( \large PBCQ \: \) вписанный. Значит \( \large \angle BCQ +\angle BPQ = 180^0 \: \), Отрезок \( \large MN \: \) — средняя линия трапеции \( \large ABCD \: \), она параллельна основанию \( \large BC \: \), а тогда \( \large \angle BCQ +\angle QNP = 180^0 \: \) как односторонние углы при параллельных прямых. Следовательно,\( \large \angle BPQ = \angle QNM \: \) Для смежных углов справедливо равенство \( \large \angle BPQ +\angle MPQ = 180^0 \: \) а значит, \( \large \angle QNM +\angle MPQ = 180^0 \: \) В четырёхугольнике \( \large MPQN \: \) сумма противоположных углов равна 180°, поэтому вокруг него можно описать окружность. Тем самым, точки \( \large M \: \), \( \large N \: \), \( \large P \: \) и \( \large Q \: \) лежат на одной окружности, что и требовалось доказать.
б)
Пусть \( \large \angle QNM = \angle QDA =\alpha \: \) (эти углы равны как соответственные углы при параллельных прямых).
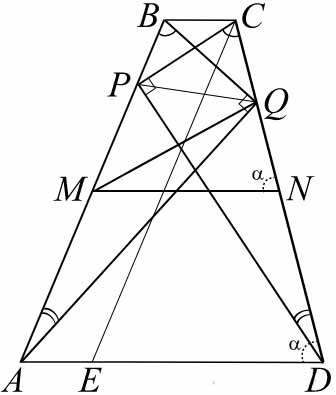
В пункте а) было показано, что \( \large \angle QNM +\angle MPQ = 180^0 \: \), это означает, что \( \large \angle QDA +\angle MPQ = 180^0 \: \) , и, следовательно, точки \( \large A \: \), \( \large D \: \), \( \large P \: \) и \( \large Q \: \) тоже лежат на одной окружности.
Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны. Следовательно, \( \large \angle BPQ =\angle PCQ \: \) и \( \large \angle PAQ =\angle PDQ \: \) . Значит, треугольники \( \large DPC \: \) и \( \large AQB \: \) подобны по двум углам. Следовательно, \( \large \angle AQB =\angle DPC =90^0 \: \), так как по условию \( \large DP \: \) и \( \large PC \: \) перпендикулярны.
В прямоугольном треугольнике \( \large AQB \: \) точка \( \large M \: \) − середина гипотенузы. Следовательно, \( \large MQ =AM =MB = \: \) \( \large \frac{AB}{2} = \frac{21}{2} =10,5 \: \). С другой стороны, средняя линия трапеции \( \large MN = \frac{AD+BC}{2} = \frac{4+17}{2} =10,5 \: \). Значит, треугольник \( \large NMQ \: \) равнобедренный и в нём \( \large QN=2\cdot MN\cdot cos\alpha = 21\cdot cos\alpha \: \). Осталось найти косинус угла \( \large CDA \: \).
Для этого на отрезке \( \large AD \: \) отметим точку \( \large E \: \), так что \( \large AE=BC=4 \: \), тогда \( \large DE=13 \: \), \( \large CE=21 \: \). Для треугольника \( \large CDE \: \) запишем теорему косинусов: \( \large CE^2 =DE^2 +CD^2- \: \) \( \large 2DE\cdot CD\cdot cos\alpha \: \), откуда выразим косинус угла \( \large CDE \: \):
\(cos\alpha = \frac{DE^2+CD^2-CE^2}{2DE\cdot CD}= \: \) \(\frac{13^2+20^2-21^2}{2\cdot 13\cdot20}=\frac{16}{65} \: \).
Итак, \( \large QN = 21cos\alpha=21\cdot \frac{16}{65} = \frac{336}{65} \: \).
Приведем другое решение пункта б):
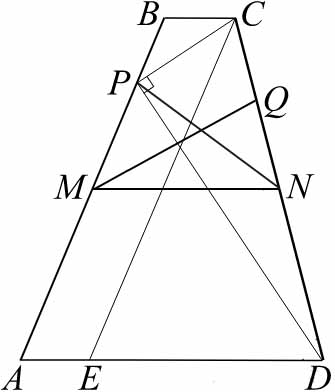
Заметим, что раз треугольник \( \large PDC \: \) — прямоугольный, то \( \large PN=CN=ND=10 \: \), \( \large MN=\frac{17+4}{2}=10,5 \: \) - средняя линия трапеции \( \large ABCD \: \). Зная боковые стороны и основания трапеции, нетрудно найти ее высоту из треугольника \( \large CED \: \) со сторонами 21, 20 и 13:
\(h=\frac{252}{13} \: \). Отсюда найдем \(sin\angle BAD = \frac{\frac{252}{13}}{21}=\frac{12}{13} \: \), \(sin\angle CDA=\frac{\frac{252}{13}}{20}=\frac{63}{65} \: \). Теперь, так как \(\angle PNM = \angle BAD \: \), по теореме синусов для треугольника \(MPN \: \), можем найти радиус окружности, описанной около \(MPQN \: \):
\(R=\frac{PN}{2sin\angle PMN}=\frac{10}{2\cdot \frac{12}{13}} = \frac{65}{12} \: \).
Так как найдем \( \large \angle QNM = \angle CDA \: \), найдем \( \large MQ \: \) по теореме синусов для треугольника \( \large MQN \: \):
\(MQ=2Rsin\angle QNM= \: \) \(2\cdot\frac{65}{12}\cdot \frac{63}{65} \: \) \( = \frac{21}{2} \: \);
Таким образом, треугольник \( \large MQN \: \) — равнобедренный:
\(QN=2\cdot MN\cdot cos\angle MNQ = \: \) \( 2\cdot \frac{21}{2}\cdot \sqrt{1-\left( \frac{63}{65}\right)^2} = \: \)
\(21\cdot \frac{\sqrt{65^2-63^2}}{65} = \frac{21}{65}\sqrt{2\cdot 128} = \: \) \(\frac{21\cdot 16}{65} =\frac{336}{65} \: \).
Ответ: б) \(\frac{336}{65}\)
Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года?
Пусть у Степана было \( \large х \: \) тыс. руб., первый банк дает \( \large а \: \)% годовых, второй — \( \large b \: \)% годовых. Тогда в конце года сумма вклада в первом банке увеличится в \( \large m=1+0,01a \: \) раз, а во втором банке в \( \large n=1+0,01b \: \) раз.
Степан положил в первый и второй банк 60% и 40% своего капитала, по прошествии одного года на счетах в банках было \( \large 0,6xm + 0,4xn =590 \: \) тыс. руб. соответственно. Если бы Степан первоначально положил 40% капитала в первый банк, а 60% капитала во второй банк, то через год на счетах было бы \( \large 0,4xm + 0,6xn =610 \: \) тыс. руб.
Решая систему уравнений:
\(\begin{cases} 0,6xm + 0,4xn =590, \\ 0,4xm + 0,6xn =610 \end{cases} \: \) относительно \(xm \: \) и \(xn \: \) находим: \(xm = 550 \: \), \(xn = 650 \: \), \(\frac{m}{n} = \frac{11}{13} \: \), \(m = \frac{11}{13}n \: \).
К концу второго года сумма вкладов достигла величины:
\(0,6xm^2 + 0,4xn^2 = \: \) \(0,6\cdot 550\cdot m+0,4\cdot 650\cdot n = \: \) \(330\cdot \frac{11}{13}n+260n \: \) \(=\frac{3630n}{13} + 260n = \: \) \(\frac{7010}{13}n \: \).
По условию, она равна 701 тыс. руб., откуда имеем:
\(\frac{7010}{13}n = 701 \Rightarrow n=1,3 \: \).
Тогда \( \large m=1,1 \: \), \( \large x=500 \: \), а искомая величина суммы вклада к концу второго года при вложении 40% капитала в первый банк и 60% во второй равна
\(0,4xm^2 + 0,6xn^2 = \: \) \(0,4\cdot 500\cdot 1,1^2 + 0,6\cdot 500\cdot 1,3^2 = \: \) \(242+507 = 749 \: \) тыс. руб.
Ответ: 749 000 руб.
Найдите все значения \( \large a \: \), при каждом из которых наименьшее значение функции
\(f(x) = x-2|x|+|x^2-2(a+1)x+a^2+2a| \: \)
больше −4?
Найдите все значения \( \large a \: \), при каждом из которых наименьшее значение функции
\(f(x) = x-2|x|+|x^2-2(a+1)x+a^2+2a| \: \)
больше −4?
Заметим, что наименьшее значение функции больше −4, если все значения функции больше −4. Заданная функция непрерывна и на бесконечностях стремится к плюс бесконечности. Поэтому при любом значении параметра она достигает своего наименьшего значения. Тогда задачу можно переформулировать так: требуется найти все значения a, при каждом из которых неравенство
\(x-2|x|+|x^2-2(a+1)x+a^2+2a| \gt -4 \: \) (*)
выполняется при всех значениях \( \large x \: \).
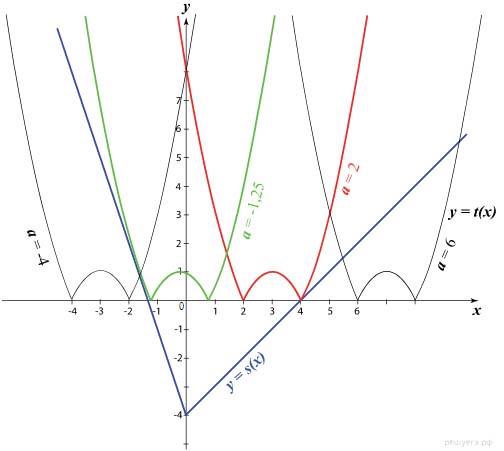
Запишем неравенство в виде
\(|(x-a)(x-a-2)| \gt -4-x+2|x| \: \),
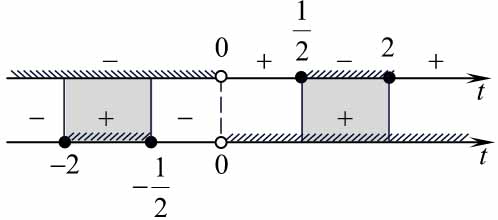
и построим графики левой и правой частей неравенства \( \large t(x) = |(x-a)(x-(a+2))| \: \) и \( \large s(x) = -4-x+2|x| \: \).
График функции \( \large t(x) \: \) — парабола с отраженной отрицательной частью, перемещающаяся по оси абсцисс, с корнями\( \large x=a \: \) и \( \large x=a+2) \: \)
График функции
\(s(x) = \begin{cases} -4-3x, при x \lt 0 \\ -4+x, при x\ge 0 \end{cases} \: \) — изображённая на рисунке ломаная (выделена синим цветом).
Для выполнения неравенства (*) необходимо, чтобы все точки графика \( \large y(x) = t(x) \: \) располагались выше графика \( \large y(x) = s(x) \: \) Граничные способы подходящего расположения подвижного графика \( \large y(x) = t(x) \: \) изображены на рисунке зелёным и красным цветом. Определим значения параметра для этих границ.
Левую границу найдём из условия касания прямой, задаваемой уравнением \( \large y=-3x-4 \: \) и параболы, задаваемой уравнением \( \large y=x^2-2(a+1)x+a^2+2a \: \). Они имеют единственную общую точку, а значит, уравнение
\(x^2-2(a+1)x+a^2+2a = -3x-4 \: \) имеет единственное решение. Запишем его в виде
\(x^2-(2a-1)x+a^2+2a+4 = 0 \: \) и найдем дискриминант полученного уравнения:
\(D=(2a-1)^2-4\cdot (a^2+2a+4) = -12a -15 \: \).
Он обращается в нуль при \( \large a=-1,25 \: \).
Правая граница достигается, если больший корень функции \( \large t(x) \: \) равен 4: \( \large a+2=4 \: \), откуда \( \large a=2 \: \).
Таким образом неравенство (*) выполняется при всех значениях \( \large x \: \), если \( \large -1,25 \lt a \lt 2 \: \).
\(-1,25 \lt a \lt 2 \: \).
Ответ: \(-1,25 \lt a \lt 2\).
а) Существуют ли двузначные натуральные числа \( \large m \: \) и \( \large n \: \) такие, что \( \large \left|\frac{m}{n}-\sqrt 2\right|\le \frac{1}{100} \: \)?
б) Существуют ли двузначные натуральные числа \( \large m \: \) и \( \large n \: \) такие, что \( \large \left|\frac{m^2}{n^2}-2\right|\le \frac{1}{10000} \: \)?
в) Найдите все возможные значения натурального числа \( \large n \: \) при каждом которых значение выражения
\(\left|\frac{n+10}{n} -\sqrt 2\right| \: \) будет наименьшим.
а) Поскольку \( \large 1,4\lt \sqrt2 \lt1 1,42 \: \), число \( \large \sqrt 2 \: \) лежит в отрезке \( \large \left[\frac{28}{27};\frac{71}{50}\right] \: \), длина которого равна \( \large \frac{71}{50} - \frac{28}{20} =\frac{1}{50} \: \). Следовательно, расстояние от \( \large \sqrt 2 \: \) до какого-то из концов отрезка не больше половины его длины. Поэтому числа \( \large m \: \) и \( \large n \: \) суть числа 28 и 20 или числа 71 и 50 соответственно. Тем самым, искомые числа существуют.
Примечание.
Заметим, что \( \large \sqrt 2 \: \) лежит правее точки 1,41 — середины отрезка \( \large \left[\frac{28}{20};\frac{71}{50}\right] \: \). Поэтому, \( \large \left|\frac{71}{50} -\sqrt 2\right| \lt \frac{1}{100} \: \). Следовательно, числа 71 и 50 являются искомым примером.
Приведем другое решение пункта а).
а) Заметим, что из неравенства \( \large \left|\frac{m}{n}-\sqrt 2\right|\le \frac{1}{100} \: \) следует, что
\(1,4 = 1,41 - \frac{1}{100} \lt \sqrt 2- \frac{1}{100} \: \) \( \le \frac{m}{n}\le \sqrt 2+ \frac{1}{100}\lt \sqrt 2+\frac{1}{100} =1,43 \: \),
а значит, \( \large 1,4n \lt m \lt 1,43n \: \) откуда \( \large \frac{m}{1,43}\lt n\lt \frac{m}{1,4} \: \).
Пусть, например, \( \large m = 99 \: \), тогда \( \large 69,2 \lt n \lt 70,7 \: \). Следовательно, двузначные числа \( \large m=99 \: \) и \( \large n=70 \: \) удовлетворяют исходному неравенству.
б) Докажем, что таких \( \large m \: \) и \( \large n \: \) не существует. Доказательство проведём от противного. Пусть существуют двузначные числа \( \large m \: \) и \( \large n \: \), для которых выполняется неравенство \( \large \left|\frac{m^2}{n^2}-2\right|\le \frac{1}{10000} \: \). Тогда
\(\frac{m^2}{n^2}-\frac{1}{100^2} \le 2 \le \frac{m^2}{n^2} + \frac{1}{100^2} \: \).
Так как по условию \( \large n\lt100 \: \), из последнего неравенства получаем
\(\frac{m^2}{n^2}-\frac{1}{n^2} \lt 2 \lt \frac{m^2}{n^2}+\frac{1}{n^2} \: \),
откуда \( \large m^2-1 \lt 2n^2 \lt m^2+1 \: \). Следовательно, \( \large 2n^2 =m^2 \: \). Противоречие.
Приведем другое решение пункта б).
Умножим обе части неравенства на \( \large n^2 \: \), получим
\(\frac{m^2}{n^2}-\frac{1}{100^2} \le 2 \le \frac{m^2}{n^2}+\frac{1}{100^2} \: \).
Так как по условию \( \large n \lt 100 \: \), из последнего неравенства получаем
\(\frac{m^2}{n^2}-\frac{1}{n^2} \lt 2 \lt \frac{m^2}{n^2}+\frac{1}{n^2} \: \),
откуда \( \large m^2-1 \lt 2n^2 \lt m^2+1 \: \). Следовательно, \( \large 2n^2 =m^2 \: \). Противоречие.
в) С увеличением \( \large n \: \) значение выражения \( \large \frac{n+10}{n} = 1 +\frac{10}{n} \: \) уменьшается. Так как при \( \large n=24 \: \) значение выражения \( \large 1 +\frac{10}{n} \: \) больше \( \large \sqrt 2 \: \), при \( \large n=25 \: \) — меньше \( \large \sqrt 2 \: \) и значение \( \large \left|\frac{n+10}{n} - \sqrt 2\right| \: \) равно расстоянию от \( \large \frac{n+10}{n} \: \) до \( \large \sqrt 2 \: \), наименьшее значение это выражение принимает при \( \large n=24 \: \) или \( \large n=25 \: \).
При \( \large n=24 \: \) получаем:
\(\left|\frac{n+10}{n} - \sqrt 2\right| = \: \) \(\frac{34}{24} - \sqrt 2 \: \),
а при \( \large n=25 \: \) получаем
\(\left|\frac{n+10}{n} - \sqrt 2\right| = \: \) \(\sqrt 2 - \frac{35}{25} \: \).
Сравнивая эти значения, видим, что наименьшее значение выражение \( \large \left|\frac{n+10}{n} - \sqrt 2\right| \: \) принимает при \( \large n=24 \: \).
Ответ: