В доме, в котором живёт Ася, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Ася живёт в квартире № 38.
В каком подъезде живёт Ася?
В доме, в котором живёт Ася, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Ася живёт в квартире № 38.
В каком подъезде живёт Ася?
В каждом подъезде по \( \large 9\cdot 3 =27 \: \) квартир. Так как \( \large 38 = 27\cdot 1 + 11 \: \) Ася живёт во 2-м подъезде.
Ответ: 2
Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит от скорости движения. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы).
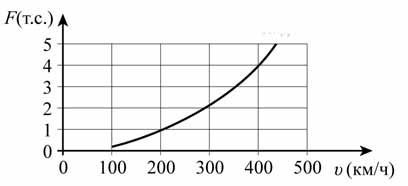
Определите по рисунку, чему равна подъёмная сила (в тоннах силы) при скорости км/ч.
Из графика видно, что при значении аргумента \( \large v=400 \: \) значение функции \( \large F(v) \: \) равно 4.
Ответ: 4
На клетчатой бумаге с размером клетки \( \large 1 \times 1 \: \) изображён треугольник \( \large ABC \: \)
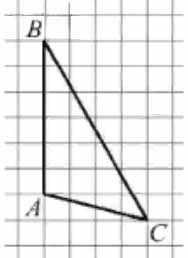
Найдите длину его средней линии, параллельной стороне \( \large AB \: \)
Средняя линия треугольника, параллельная стороне \( \large AB \: \) равна половине \( \large AB \: \). Так как \( \large AB = 6 \: \), то длина средней линии равна \( \large 6:2=3 \: \).
Ответ: 3
В классе 9 учащихся, среди них два друга — Михаил и Андрей. Учащихся случайным образом разбивают на 3 равные группы.
Найдите вероятность того, что Михаил и Андрей окажутся в одной группе.
Число учащихся в каждой группе равно \( \large 9:3 = 3 \: \). Допустим, один из друзей попал в одну из таких групп. Тогда в этой группе остаётся ещё 2 свободных места, на которых может оказаться второй друг. Всего есть 8 учеников, которые могут занять эти места. Поэтому искомая вероятность равна \( \large \frac{2}{8} \: \)
Ответ: 0,25
Найдите корень уравнения \( \large \frac{1}{9x+5} = \frac{1}{4x+6} \: \)
Из равенства двух дробей вытекает, что \( \large 9x+5 = 4x+6 \: \) при условии, что ни левая, ни правая часть этого уравнения не обращается в нуль.
Отсюда получим \( \large 5x =1 \: \), \( \large x = 0,2 \: \)
Ответ: 0,2
Площадь параллелограмма \( \large ABCD \: \) равна 36. Точка \( \large E \: \) — середина стороны \( \large CD \: \). Найдите площадь трапеции \( \large ABDE \: \).
Проведём высоту параллелограмма из вершины \( \large B \: \) к продолжению стороны \( \large CD \: \). Площадь трапеции \( \large ABDE \: \) равна разности площадей параллелограмма \( \large ABCD \: \) и треугольника \( \large BCE \: \).
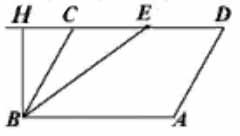
Имеем:
\(S_{ABCD} = CD\cdot BH \: \),
\(S_{BCE} = \frac{1}{2} \cdot CE\cdot BH = \frac{1}{2}\cdot \frac {1}{2} cdot CD\cdot BH = \frac{1}{4}\cdot S_{ABCD} = \frac{1}{4}\cdot 36 =9 \: \)
\(S_{ABED} = 36 -9 = 27 \: \)
Ответ: 27
На рисунке изображены график функции \( \large y=f(x) \: \) и касательная к нему в точке с абсциссой \( \large x_0 \: \).
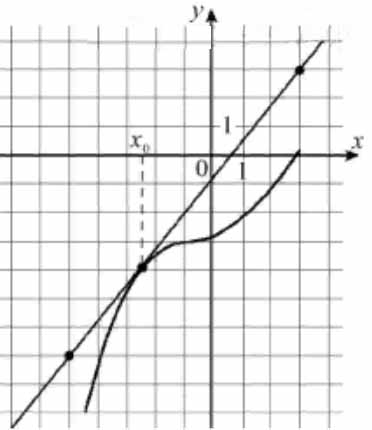
Найдите значение производной функции \( \large f(x) \: \) в точке \( \large x_0 \: \).
Пусть угол, который образует касательная с положительным направлением оси абсцисс, равен \( \large \alpha \: \), а угловой коэффициент касательной равен \( \large k \: \), т. е. \( \large k=tg\alpha \: \). Значение производной в точке касания равно угловому коэффициенту касательной, проведённой в этой точке, т.е. равно тангенсу угла \( \large \alpha \: \).
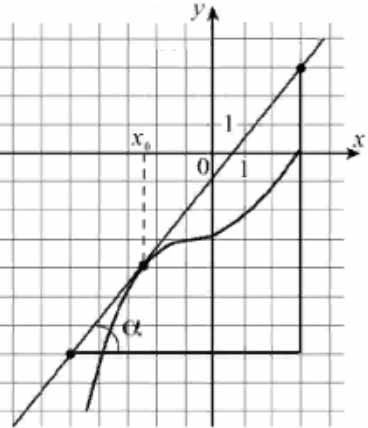
Из построенного прямоугольного треугольника находим: \( \large y'=tg\alpha =\frac{10}{8} = 1,25 \: \).
Ответ: 1,25
В правильной четырёхугольной призме \( \large ABCDA_1B_1C_1D_1 \: \) известно, что \( \large DB_1 = 2C_1D_1 \: \). Найдите угол между диагоналями \( \large BD_1 \: \) и \( \large AC_1 \: \). Ответ дайте в градусах.
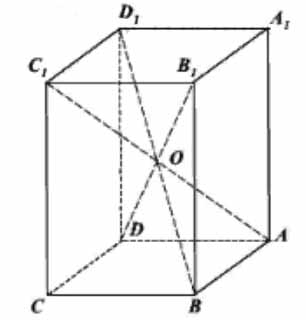
Пусть \( \large DB_1 \: \) и \( \large BD_1 \: \) пересекаются в точке \( \large O \: \). Так как правильная четырёхугольная призма является прямоугольным параллелепипедом, а диагонали прямоугольного параллелепипеда равны, то \( \large BD_1=DB_1=2C_1D \: \), то есть \( \large C_1D_1 = \frac{1}{2}BD_1 \: \). По свойству параллелепипеда получим также, что \( \large O \: \) – середина диагоналей призмы, т. е. \( \large OC_1 = OD_1 =\frac{1}{2}BD_1 \: \). Тогда \( \large C_1D_1 = \frac{1}{2}BD_1 = OD_1 = OC_1 \: \).
Значит, треугольник \( \large OC_1D_1 \: \) равносторонний, и угол \( \large C_1OD_1 =60^0 \: \).
Ответ: 60
Найдите значение выражения \( \large 36\sqrt{3}\cdot tg\frac{\pi}{3}sin\frac{\pi}{6} \: \)
Найдите значение выражения \( \large 36\sqrt{3}\cdot tg\frac{\pi}{3}sin\frac{\pi}{6} = \: \) \( \large 36\sqrt{3}\cdot \sqrt{3}\cdot \frac{1}{2} = 54 \: \)
Ответ: 54
Для определения эффективной температуры звёзд используют закон Стефана—Больцмана,, согласно которому \( \large P= \sigma ST^4 \: \), где \( \large P \: \)— мощность излучения звезды (в ваттах), \( \large \sigma = 5,7\cdot 10^{-8} \frac{Вт}{м^2\cdot K^4} \: \)— постоянная, \( \large S \: \) — площадь поверхности звезды (в квадратных метрах), а \( \large T \: \) — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна \( \large \frac{1}{64}\cdot 10^{20} \: \) м 2, а мощность её излучения равна \( \large 2,28\cdot 10^{25} \: \) Вт.
Найдите температуру этой звезды в кельвинах.
\(2,28 \cdot 10^{25} = 5,7\cdot 10^{-8}\cdot \frac{1}{64}\cdot 10^{20}\cdot T^4 \: \)
\(0,4\cdot 10^{13} \cdot 64= T^4 \: \)
\( 4 \cdot 10^{12}\cdot 64 =T^4 \: \)
\( 256\cdot 10^{12} =T^4 \: \)
\(4\cdot 10^3 = T \: \)
Ответ: 4000
Автомобиль выехал с постоянной скоростью 72 км/ч из города A в город B, расстояние между которыми равно 360 км. Одновременно с ним из города C в город B, расстояние между которыми равно 270 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 30 минут. В результате автомобиль и мотоцикл прибыли в город B одновременно.
Найдите скорость мотоциклиста.
Ответ дайте в км/ч.
Пусть \( \large x \: \) (км/час) - скорость мотоциклиста. От А до В автомобилье ехал \( \large \frac{360}{72} \: \) часов, а мотоциклист из С в В (если бы он только ехал, неостанавливаясь): \( \large \frac{270}{x} \: \), но с учетом остановки: \( \large \frac{270}{x} + \frac{1}{2} \: \). Выехали одновременно, приехали одновременно. т.е.:
$$ \frac{360}{72} = \frac{270}{x} + \frac{1}{2} $$Начнем решать: \( \large 5\cdot 2\cdot x = 270\cdot 2+1\cdot x \Leftrightarrow \: \) \( \large 10\cdot x = 540 + x \Leftrightarrow \: \) \( \large 9\cdot x = 540 \Leftrightarrow \: \) \( \large x = 60 \: \)Ответ: 60
Найдите наибольшее значение функции \( \large y=-\frac{5x^2+12x}{x} \: \) на отрезке \( \large \left[-10,-1\right] \: \).
Воспользуемся правилом нахождения производных: \( \large y' = \left( \frac{u}{v}\right)' = \frac{u'\cdot v-u\cdot v'}{v^2} = \: \) \( \large -\frac{(10x+12)\cdot x - (5x^2+12x)\cdot x'}{x^2} = \: \) \( \large -\frac{5x^2}{x^2} = -5 \: \)
Так как \( \large y' < 0 \: \), функция \( \large y \: \) убывает на всей области определения: \( \large x \in (-\infty; 0) \cup (0;+\infty ) \: \). Значит, наибольшее значение функции достигается на левой границе заданного отрезка \( \large x=-10 \: \).
Подставляем \( \large x=-10 \: \) в исходную функцию:
\( y=-\frac{5(-10)^2+12\cdot(-10)}{-10} = -\frac{380}{-10} = 38 \: \)
Можно было бы решить проще: \( \large y=-\frac{5x^2+12x}{x} = -5x - 12 \: \), но предварительно заметив, что \( \large x \neq 0 \: \). Это линейная убывающая функция. Подставляем в нее \( \large x=-10 \: \), получаем \( \large y = -5\cdot(-10) -12 =50-12 = 38 \: \).
Ответ: 38
а) Решите уравнение \( \large \sqrt 3 \cdot tg(5\pi+2x) = 3 \: \).
б) Укажите корни этого уравнения, принадлежащие отрезку \( \large \left[\pi; \frac{5\pi}{2} \right] \: \).
а) Так как период у \( \large tg\alpha \: \) равен \( \large \pi \: \), то \( \large tg(5\pi+2x) = tg(2x) \: \) и тогда получим уравнение:
\(\sqrt 3 \cdot tg(2x) = 3 \Leftrightarrow \: \) \( tg(2x) = \frac{3}{\sqrt 3} \Leftrightarrow \: \) \(tg(2x) = \sqrt 3 \Leftrightarrow \: \) \(2x = \frac{\pi}{3} + \pi\cdot n, n \in Z \Leftrightarrow \: \) \(x = \frac{\pi}{6} + \frac{\pi}{2}\cdot n, n \in Z \: \)
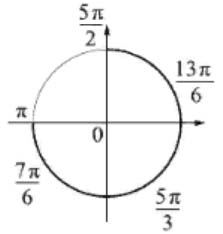
б) Отметим на числовой окружности дугу, соответствующую промежутку \( \large \left[\pi; \frac{5\pi}{2} \right] \: \). На ней отметим точки, соответствующие решению: \( \large x = \frac{\pi}{6} + \frac{\pi}{2}\cdot n \: \), т.е. \( \large \pi+\frac{\pi}{6} = \frac{7\pi}{6} \: \), \( \large \frac{7\pi}{6}+\frac{\pi}{2} = \frac{10\pi}{6} \: \), \( \large \frac{10\pi}{6}+\frac{\pi}{2} = \frac{13\pi}{6} \: \). По картинке видно, что если мы к этому корню прибавим еще раз \( \large \frac{\pi}{2} \: \), то он выдет за указанный отрезок. Таким образом, получаем: \( \large \frac{7\pi}{6} \: \), \( \large \frac{5\pi}{3} \: \), \( \large \frac{13\pi}{6} \: \).
Ответ: а) \(x = \frac{\pi}{6} + \frac{\pi}{2}\cdot n, n \in Z \) б) \(\frac{7\pi}{6}\), \(\frac{5\pi}{3}\), \(\frac{13\pi}{6}\)
Точки \( \large P \: \) и \( \large Q \: \) - середины ребер \( \large AD \: \) и \( \large CC_1 \: \) куба \( \large ABCDA_1B_1C_1D_1 \: \) соответственно.
а) Докажите, что прямая \( \large BQ \: \) перпендикулярна прямой \( \large B_1P \: \).
б) Пусть \( \large H \: \) - проекция точки \( \large Q \: \) на прямую \( \large B_1P \: \). Найдите \( \large B_1H \: \), если \( \large AB=24 \: \).
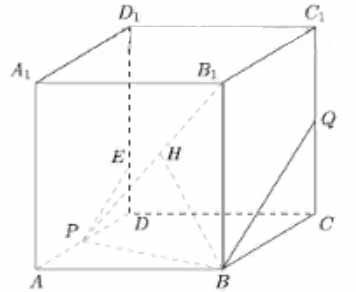
а) Пусть ребро куба равно \( \large 4a \: \). Отметим на ребре \( \large DD_1 \: \) такую точку \( \large E \: \), что \( \large DE = a \: \). Прямая \( \large PE \: \) параллельна прямой \( \large BQ \: \), следовательно необходимо проверить, что \( \large \angle EPB_1 =90^0 \: \).
По теореме Пифагора вычислим длину стороны треугольника \( \large EPB_1 \: \):
\(PE^2 = PD^2+DE^2=5a^2. \: \)
\(B_1E^2 =B_1D_1^2+D_1E^2=32a^2+9a^2=41a^2 \: \)
\(B_1P=D_1B^2+BA^2+AP^2=16a^2+16a^2+4a^2=36a^2 \: \),
\(B_1P=6a \: \).
а) Поскольку \( \large 5a^2+36a^2=41a^2=B_1E^2=PE^2+B_1P^2 \: \), по теореме, обратной теореме Пифагора, получаем, что \( \large EPB_1=90^0 \: \), т.е. прямая \( \large BQ \: \) перпендикулярна прямой \( \large B_1P \: \).
б) Поскольку прямая \( \large BQ \: \) перпендикулярна прямой \( \large B_1P \: \), проекции точек \( \large B \: \) и \( \large Q \: \) на прямую \( \large B_1P \: \) совпадают. В прямоугольном треугольнике \( \large BB_1P \: \) имеем:
\(cos \angle HB_1B=\frac{HB_1}{B_1B}=\frac{B_1B}{PB_1} \: \), откуда \(HB_1=\frac{B_1B^2}{PB_1}=\frac{576}{36} =16 \: \).
Другое решение:
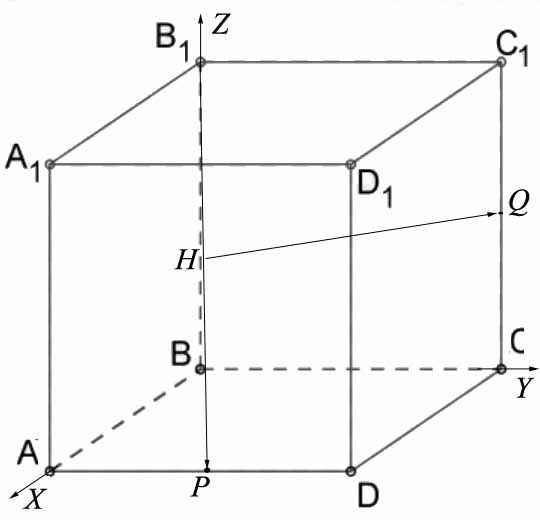
Введем систему координат с центром в точке \( \large B \: \). Оси \( \large X \: \), \( \large Y \: \), \( \large Z \: \) направим соответственно вдоль ребер куба \( \large BA \: \), \( \large BC \: \),\( \large BB_1 \: \). Пусть длина ребра куба равна \( \large a \: \). Тогда координаты точек \( \large B_1(0,0,a) \: \), \( \large P(0,\frac{a}{2}, 0) \: \), \( \large Q(0,a,\frac{a}{2}) \: \). Следовательно, \( \large \overrightarrow{B_1P}(a,\frac{a}{2},-a) \: \), \( \large \overrightarrow{BQ}(0,a,\frac{a}{2}) \: \). Их скалярное произведение:
\(\overrightarrow{BQ}(0,a,\frac{a}{2}) \cdot \overrightarrow{BQ}(0,a,\frac{a}{2}) = a\cdot 0+ \frac{a}{2}\cdot a+ (-a)\cdot \frac{a}{2} = 0 \: \). Следовательно, они перпендикулярны.
б) Уравнение прямой \( \large B_1P \: \), проходящей через две точки, имеет вид:
$$\frac{x}{a} = \frac{y}{\frac{a}{2}} = \frac{z-a}{-a}$$Откуда
$$\begin{cases}z=-x+a \\y=\frac{1}{2}\cdot x\end{cases}\;(1)$$Путь точка \( \large H \: \) - проекция точки \( \large Q \: \) на эту прямую, т.е. точка \( \large H \: \) лежит на прямой, а значит, ее координаты удовлетворяют уравнению прямой \( \large B_1P \: \), с одной стороны, а с другой, вектор \( \large \overrightarrow{B_1P} \perp \overrightarrow{QH}(x_h,y_h-a,z_h-\frac{a}{2}) \: \), т.е. их скаляное произведение равно нулю:
$$ a\cdot x_h+\frac{a}{2}\cdot (y_h-a)+(-a)\cdot (z_h-\frac{a}{2}) =0 $$Подставляем в это уравнение координаты точки \( \large H \: \), выраженные (1):$$ a\cdot x_h+\frac{a}{2}\cdot \left( \frac{1}{2}\cdot x_h-a \right)+(-a)\cdot \left(-x_h+a -\frac{a}{2}\right) =0 $$Найдем:
\(x_h=\frac{4a}{9} \Rightarrow y_h=\frac{2a}{9}, z_h=\frac{5a}{9} \: \)
Тогда расстояние \( \large HB_1 =\sqrt{\left(0 - \frac{4a}{9}\right)^2+\left(0 - \frac{2a}{9}\right)^2+\left(a - \frac{5a}{9}\right)^2} = \: \) \( \large \sqrt{\left( \frac{16a^2}{81}\right)+\left( \frac{4a^2}{81}\right)+\left( \frac{16a^2}{81}\right)} = \: \)
\(\sqrt{\frac{36a^2}{81}} =\frac{6a}{9} =\frac{6\cdot 24}{9} =16 \: \)
Ответ: б) 16
Решите неравенство: \( \large \frac{4x^4-4x^3+x^2}{-2x^2+5x-2} +\frac{2x^3 -7x^2+5x+1}{x-2} \le 0 \: \)
Ответ: